
【题目】已知函数![]() .
.
(1)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)若![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() 有唯一零点,证明:
有唯一零点,证明:![]() .
.
【答案】(1)见解析;(2)证明见解析
【解析】
(1)求导后得![]() ,再对
,再对![]() 分四种情况讨论可得函数的单调性;
分四种情况讨论可得函数的单调性;
(2)令![]() =0,可知
=0,可知![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,所以
,所以![]() ①, 要使
①, 要使![]() 在
在![]() 上恒成立,且
上恒成立,且![]() 有唯一解,只需
有唯一解,只需![]() ,即
,即![]() ②,再联立①②可知,
②,再联立①②可知,![]() ,然后构造函数,利用导数可得.
,然后构造函数,利用导数可得.
(1)依题意,![]()
若![]() ,则
,则![]() ,
,
故函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,令
,令![]() ,解得
,解得![]() ;
;
若![]() ,则
,则![]() ,则
,则![]() ,
,
函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,则
,则![]() ,则
,则![]() ,
,
则函数![]() 在
在![]() 上单调递减;
上单调递减;
若![]() ,则
,则![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
综上所述,![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)依题意,![]() ,而
,而![]() ,
,
令![]() ,解得
,解得![]() ,
,
因为![]() ,故
,故![]() ,
,
故![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ;
;
又![]() ,
,
故![]() ①,
①,
要使![]() 在
在![]() 上恒成立,且
上恒成立,且![]() 有唯一解,
有唯一解,
只需![]() ,即
,即![]() ②,
②,
由①②可知,![]()
令![]()
显然![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() ,
,
故![]() ,
,
又![]() 在
在![]() 上单调递增,
上单调递增,
故必有![]()


科目:高中数学 来源: 题型:
【题目】已知不等式![]() .
.
(1)是否存在实数m,使不等式对任意![]() 恒成立?并说明理由.
恒成立?并说明理由.
(2)若不等式对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)若对于![]() ,不等式恒成立,求实数x的取值范围.
,不等式恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,底面为边长为
中,底面为边长为![]() 的正三角形,
的正三角形,![]() 在底面的射影为
在底面的射影为![]() 中点且
中点且![]() 到底面的距离为
到底面的距离为![]() ,已知
,已知![]() 分别是线段
分别是线段![]() 与
与![]() 上的动点,记线段
上的动点,记线段![]() 中点
中点![]() 的轨迹为
的轨迹为![]() ,则
,则![]() 等于( )(注:
等于( )(注:![]() 表示
表示![]() 的测度,本题中
的测度,本题中![]() 若分别为曲线、平面图形、空间几何体,分别对应为其长度、面积、体积)
若分别为曲线、平面图形、空间几何体,分别对应为其长度、面积、体积)
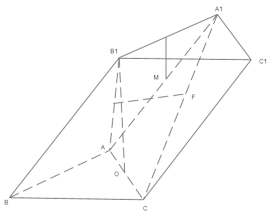
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]() ,使得函数
,使得函数![]() 满足以下两个条件:(1)
满足以下两个条件:(1)![]() 在[m,n]上是单调函数;(2)
在[m,n]上是单调函数;(2)![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有( )个.
的“倍值区间”.下列函数中存在“倍值区间”的有( )个.
①![]() ②
②![]() ③
③![]()
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC≠60°,过点B、C分别作△ABC外接圆的切线BD、CE,且满足![]() ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当![]() 时,y是x的二次函数;当
时,y是x的二次函数;当![]() 时,
时,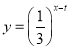 测得数据如下表(部分):
测得数据如下表(部分):
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式![]() ;
;
(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (e为自然对数的底数,e=2.71828……),函数
(e为自然对数的底数,e=2.71828……),函数![]() 图象关于直线
图象关于直线![]() 对称,函数
对称,函数![]() 的最小值为m.
的最小值为m.
(I)求曲线![]() 的切线方程;
的切线方程;
(Ⅱ)求证:![]() ;
;
(III)求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC=BC=PC=2,AB=PA=PB=2![]() .
.
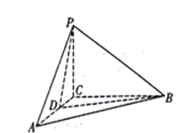
(1)证明:PC⊥平面ABC;
(2)若点D在棱AC上,且二面角D-PB-C为30°,求PD与平面PAB所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com