
【题目】如图所示的四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() 的中点为
的中点为![]() ,
, ![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,
, ![]() 平面
平面![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值的大小.
的余弦值的大小.

【答案】(1)见解析.(2)![]() .
.
【解析】试题分析:(1)由已![]() 为矩形,可得
为矩形,可得![]() 为
为![]() 的中点.结合
的中点.结合![]() 为
为![]() 的中点,根据三角形中位线定理可得,
的中点,根据三角形中位线定理可得, ![]() ,由线面平行的判定定理可得结果;(2)由(1)可知
,由线面平行的判定定理可得结果;(2)由(1)可知![]() ,所以
,所以![]() 或
或![]() ,先证明
,先证明![]() ,可得
,可得![]() ,因为
,因为![]() ,
, ![]() ,
, ![]() 两两垂直,分别以
两两垂直,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,平面
轴建立空间直角坐标系,平面![]() 的一个法向量为
的一个法向量为![]() ,再求出平面
,再求出平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果.
的一个法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)由已知![]() 为矩形,且
为矩形,且![]() ,所以
,所以![]() 为
为![]() 的中点.
的中点.
又因为![]() 为
为![]() 的中点,所以在
的中点,所以在![]() 中,
中, ![]() ,又因为
,又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() .
.
(2)由(1)可知![]() ,所以异面直线
,所以异面直线![]() 与
与![]() 所成的角即为
所成的角即为![]() (或
(或![]() 的补角).
的补角).
所以![]() 或
或![]() .
.
设![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,又由
,又由![]() 平面
平面![]() 可知
可知![]() ,且
,且![]() 为中点,因此
为中点,因此![]() ,此时
,此时![]() ,所以
,所以![]() ,所以
,所以![]() 为等边三角形,所以
为等边三角形,所以![]() ,即
,即![]() ,因为
,因为![]() ,
, ![]() ,
, ![]() 两两垂直,分别以
两两垂直,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,如图所示,
轴建立空间直角坐标系,如图所示,

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() .
.
由![]() ,
, ![]() ,
, ![]() ,可得
,可得![]() 平面
平面![]() ,可取平面
,可取平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由
令![]() ,所以
,所以![]() .
.
因此  ,又二面角
,又二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有200户农民,且都从事水果种植,据了解,平均每户的年收入为3万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A袋中有1个红球和1个黑球,B袋中有2个红球和1个黑球,A袋中任取1个球与B袋中任取1个球互换,这样的互换进行了一次,求:
(1)A袋中红球恰是1个的概率;
(2)A袋中红球至少是1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件![]() “取出的两球同色”,
“取出的两球同色”,![]() “取出的2球中至少有一个黄球”,
“取出的2球中至少有一个黄球”,![]() “取出的2球至少有一个白球”,
“取出的2球至少有一个白球”,![]() “取出的两球不同色”,
“取出的两球不同色”,![]() “取出的2球中至多有一个白球”.下列判断中正确的序号为________.
“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①![]() 与
与![]() 为对立事件;②
为对立事件;②![]() 与
与![]() 是互斥事件;③
是互斥事件;③![]() 与
与![]() 是对立事件:④
是对立事件:④![]() ;⑤
;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
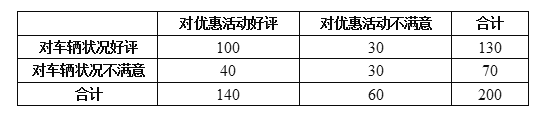
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了5张骑行券,其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友,求选取的张中至少有1张是一元券的概率.
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过转赠给好友.某用户共获得了5张骑行券,其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友,求选取的张中至少有1张是一元券的概率.

参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量![]() =(a,
=(a,![]() b)与
b)与![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a=![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上的一个最低点为
的图象上的一个最低点为![]() ,周期为
,周期为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)将![]() 的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),然后再将所得的图象沿
的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),然后再将所得的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,写出函数
的图象,写出函数![]() 的解析式;
的解析式;
(3)当![]() 时,求函数
时,求函数![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com