
【题目】已知函数f(x)=x+ ![]() ﹣1(x≠0),k∈R.
﹣1(x≠0),k∈R.
(1)当k=3时,试判断f(x)在(﹣∞,0)上的单调性,并用定义证明;
(2)若对任意x∈R,不等式f(2x)>0恒成立,求实数k的取值范围;
(3)当k∈R时,试讨论f(x)的零点个数.
【答案】
(1)解:当k=3,x∈(﹣∞,0)时,f(x)=x﹣ ![]() ,
,
![]() >0,
>0,
∴f(x)在(﹣∞,0)上单调递增.
证明:在(﹣∞,0)上任取x1,x2,令x1<x2,
f(x1)﹣f(x2)=( ![]() )﹣(
)﹣( ![]() )=(x1﹣x2)(1+
)=(x1﹣x2)(1+ ![]() ),
),
∵x1,x2∈(﹣∞,0),x1<x2,∴ ![]() ,
,
∴f(x1)﹣f(x2)<0,
∴f(x)在(﹣∞,0)上单调递增
(2)解:设2x=t,则t>0,f(t)=t+ ![]() ,
,
①当k>0时,f′(t)=1﹣ ![]() ,
,
t= ![]() 时,f′(t)=0,且f(t)取最小值,
时,f′(t)=0,且f(t)取最小值,
f( ![]() )=
)= ![]() =2
=2 ![]() ﹣1,
﹣1,
当k ![]() 时,f(
时,f( ![]() )=2
)=2 ![]() ﹣1>0,
﹣1>0,
当0<k≤ ![]() 时,f(
时,f( ![]() )=2
)=2 ![]() ﹣1≤0,
﹣1≤0,
∴k> ![]() 时,f(2x)>0成立;0<k≤
时,f(2x)>0成立;0<k≤ ![]() 时,f(2x)>0不成立.
时,f(2x)>0不成立.
②当k=0时,f(t)=t﹣1,
∵t∈(0,+∞),不满足f(t)恒大于0,∴舍去.
③当k<0时,f ![]() 恒大于0,
恒大于0,
∵ ![]() ,且f(x)在(0,+∞)内连续,
,且f(x)在(0,+∞)内连续,
∴不满足f(t)>0恒成立.
综上,k的取值范围是( ![]() ,+∞)
,+∞)
(3)解:①当k=0时,f(x)=x﹣1,有1个零点.
②当k>0时,
(i)当x>0时,f(x)=x+ ![]() ﹣1,f′(x)=1﹣
﹣1,f′(x)=1﹣ ![]() ,
,
当x= ![]() 时,f(x)取极小值,且f(x)在(0,+∞)内先减后增,
时,f(x)取极小值,且f(x)在(0,+∞)内先减后增,
由f(x)函数式得 ![]() ,
,
f( ![]() )=2
)=2 ![]() ﹣1,
﹣1,
当k= ![]() 时,f(
时,f( ![]() )=0,f(x)在(0,+∞)内有1个零点,
)=0,f(x)在(0,+∞)内有1个零点,
当k> ![]() 时,f(
时,f( ![]() )>0,f(x)在(0,+∞)内有0个零点,
)>0,f(x)在(0,+∞)内有0个零点,
当0<k< ![]() 时,f(
时,f( ![]() )<0,f(x)在(0,+∞)内有2个零点.
)<0,f(x)在(0,+∞)内有2个零点.
(ii)当x<0时,f(x)=x﹣ ![]() ﹣1,f′(x)=1+
﹣1,f′(x)=1+ ![]() ,
,
f′(x)恒大于0,∴f(x)在(﹣∞,0)单调递增,
由f(x)表达式,得: ![]() ,
, ![]() ,
,
∴f(x)在(﹣∞,0)内有1个零点.
综上,当k=0时,f(x)有1个零点;当0<k< ![]() 时,f(x)有3个零点;当k=
时,f(x)有3个零点;当k= ![]() 时,f(x)有2个零点;当k>
时,f(x)有2个零点;当k> ![]() 时,f(x)有1个零点.
时,f(x)有1个零点.
③当k<0时,同理k>0的情况:
当﹣ ![]() <k<0时,f(x)有3个零点;当k=﹣
<k<0时,f(x)有3个零点;当k=﹣ ![]() 时,f(x)有2个零点;当k<﹣
时,f(x)有2个零点;当k<﹣ ![]() 时,f(x)有1个零点.
时,f(x)有1个零点.
综上所述,当k=0或k> ![]() 或k<﹣
或k<﹣ ![]() 时,f(x)有1个零点;
时,f(x)有1个零点;
当k= ![]() 或k=﹣
或k=﹣ ![]() 时,f(x)有2个零点;
时,f(x)有2个零点;
当0<k< ![]() 或﹣
或﹣ ![]() <k<0时,f(x)有3个零点
<k<0时,f(x)有3个零点
【解析】(1)当k=3,x∈(﹣∞,0)时,f(x)=x﹣ ![]() ,
, ![]() >0,f(x)在(﹣∞,0)上单调递增.利用定义法能进行证明.(2)设2x=t,则t>0,f(t)=t+
>0,f(x)在(﹣∞,0)上单调递增.利用定义法能进行证明.(2)设2x=t,则t>0,f(t)=t+ ![]() ,根据k>0,k=0,k<0三个情况进行分类讨论经,能求出k的取值范围.(3)根据k=0,k>0,k<0三种情况分类讨论,利用导数性质能求出f(x)的零点个数.
,根据k>0,k=0,k<0三个情况进行分类讨论经,能求出k的取值范围.(3)根据k=0,k>0,k<0三种情况分类讨论,利用导数性质能求出f(x)的零点个数.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD(如图1),AB=4,AD=2,∠DAB=60°,E为AB的中点,把三角形ADE沿DE折起至A1DE位置,使得A1C=4,F是线段A1C的中点(如图2). 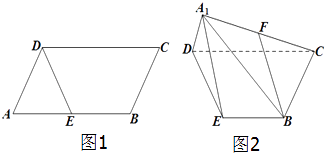
(1)求证:BF∥面A1DE;
(2)求证:面A1DE⊥面DEBC;
(3)求二面角A1﹣DC﹣E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图. 
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x满足x2﹣5x+6≤0
(1)若a=1,且q∧p为真,求实数x的取值范围;
(2)若p是q必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个平面垂直,下列命题: ①一个平面内的已知直线必垂直于另一个平面内的任意一条直线.
②一个平面内的已知直线必垂直于另一个平面内的无数条直线.
③一个平面内的任一条直线必垂直于另一个平面.
④一个平面内垂直于交线的直线与另一个平面垂直.
其中正确命题的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式组  表示的平面区域为D,则
表示的平面区域为D,则
(1)z=x2+y2的最小值为 .
(2)若函数y=|2x﹣1|+m的图象上存在区域D上的点,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对任意平面向量 ![]() =(x,y),把
=(x,y),把 ![]() 绕其起点沿逆时针方向旋转θ角得到的向量
绕其起点沿逆时针方向旋转θ角得到的向量 ![]() =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
=(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
(1)已知平面内点A(2,3),点B(2+2 ![]() ,1).把点B绕点A逆时针方向旋转
,1).把点B绕点A逆时针方向旋转 ![]() 角得到点P,求点P的坐标.
角得到点P,求点P的坐标.
(2)设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转 ![]() 后得到的点的轨迹方程是曲线y=
后得到的点的轨迹方程是曲线y= ![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com