
【题目】如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,沿对角线
,沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 内的射影
内的射影![]() 恰在
恰在![]() 上.
上.


(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)建立空间直角坐标系,利用向量的方法证明![]() ,可得AB⊥CD,再利用AB⊥BC,可得AB⊥平面BCD;
,可得AB⊥CD,再利用AB⊥BC,可得AB⊥平面BCD;
(Ⅱ)求出 ,利用向量夹角公式,可求异面直线BC与AD所成的角;
,利用向量夹角公式,可求异面直线BC与AD所成的角;
(Ⅲ)求出平面ACD的法向量 ,平面ABD的法向量
,平面ABD的法向量![]() ,利用向量夹角公式,可求二面角B﹣AD﹣C的平面角;
,利用向量夹角公式,可求二面角B﹣AD﹣C的平面角;
(Ⅰ)在梯形ABCD中,∵![]() ,∴AC2+DC2=AD2,∴AC⊥DC.
,∴AC2+DC2=AD2,∴AC⊥DC.
又BO⊥平面ACD,AC平面ACD,∴BO⊥AC,又AB=CB,∴O为AC中点.
以O为坐标原点,以OA,OB所在直线分别为x,z轴,以过O且平行于CD的直线为y轴建立空间直角坐标系.
则 ,
,
∴ ,
,![]() ,∴
,∴![]() ,∴AB⊥CD,
,∴AB⊥CD,
又AB⊥BC,BC∩CD=C,∴AB⊥平面BCD;
(Ⅱ)∵ ,∴
,∴![]() ,
,
∴![]() ,即异面直线BC与AD所成的角为60°;
,即异面直线BC与AD所成的角为60°;
(Ⅲ)平面ACD的法向量为 .
.
设平面ABD的法向量为![]() ,则
,则 ,即
,即 ,解得
,解得![]() ,取z=1,∴
,取z=1,∴![]() .
.
设二面角B .
.


科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 上的一点
上的一点![]() 作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足
作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足![]() ,
,![]() ,线段QD与
,线段QD与![]() 交于点P.
交于点P.

(1)当点P在抛物线C上,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时值金秋十月,正是秋高气爽,阳光明媚的美好时刻。复兴中学一年一度的校运会正在密锣紧鼓地筹备中,同学们也在热切地期盼着,都想为校运会出一份力。小智同学则通过对学校有关部门的走访,随机地统计了过去许多年中的五个年份的校运会“参与”人数及相关数据,并进行分析,希望能为运动会组织者科学地安排提供参考。
附:①过去许多年来学校的学生数基本上稳定在3500人左右;②“参与”人数是指运动员和志愿者,其余同学均为“啦啦队员”,不计入其中;③用数字1、2、3、4、5表示小智同学统计的五个年份的年份数,今年的年份数是6;
统计表(一)
年份数x | 1 | 2 | 3 | 4 | 5 |
“参与”人数(y千人) | 1.9 | 2.3 | 2.0 | 2.5 | 2.8 |
统计表(二)
高一(3)(4)班参加羽毛球比赛的情况:
男生 | 女生 | 小计 | |
参加(人数) | 26 | b | 50 |
不参加(人数) | c | 20 | |
小计 | 44 | 100 |
(1)请你与小智同学一起根据统计表(一)所给的数据,求出“参与”人数y关于年份数x的线性回归方程![]() ,并预估今年的校运会的“参与”人数;
,并预估今年的校运会的“参与”人数;
(2)学校命名“参与”人数占总人数的百分之八十及以上的年份为“体育活跃年”.如果该校每届校运会的“参与”人数是互不影响的,且假定小智同学对今年校运会的“参与”人数的预估是正确的,并以这6个年份中的“体育活跃年”所占的比例作为任意一年是“体育活跃年”的概率。现从过去许多年中随机抽取9年来研究,记这9年中“体活跃年”的个数为随机变量![]() ,试求随机变量
,试求随机变量的分布列、期望
![]() 和方差
和方差![]() ;
;
(3)根据统计表(二),请问:你能否有超过60%的把握认为“羽毛球运动”与“性别”有关?
参考公式和数据一: ,
,![]() ,
,![]() ,
,![]()
参考公式二: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如下表所示:
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
参考公式: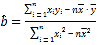 ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学宣传部组织了这样一个游戏项目:甲箱子里面有3个红球,2个白球,乙箱子里面有1个红球,2个白球,这些球除了颜色以外,完全相同。每次游戏需要从这两个箱子里面各随机摸出两个球.
(1)设在一次游戏中,摸出红球的个数为![]() ,求
,求![]() 分布列.
分布列.
(2)若在一次游戏中,摸出的红球不少于2个,则获奖.
①求一次游戏中,获奖的概率;
②若每次游戏结束后,将球放回原来的箱子,设4次游戏中获奖次数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com