
【题目】已知函数f(x)=2sin(2x﹣ ![]() ),x∈R.
),x∈R. 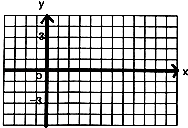
(1)在给定的平面直角坐标系中,画函数f(x)=2sin(2x﹣ ![]() ),x∈[0,π]的简图;
),x∈[0,π]的简图;
(2)求f(x)=2sin(2x﹣ ![]() ),x∈[﹣π,0]的单调增区间;
),x∈[﹣π,0]的单调增区间;
(3)函数g(x)=2cos2x的图象只经过怎样的平移变换就可得到f(x)=2sin(2x﹣ ![]() ),x∈R的图象?
),x∈R的图象?
【答案】
(1)解:对于 函数f(x)=2sin(2x﹣ ![]() ),x∈R,由x∈[0,π],可得2x﹣
),x∈R,由x∈[0,π],可得2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],列表如下:
],列表如下:
2x﹣ | ﹣ | 0 |
| π |
|
|
x | 0 |
|
|
|
| π |
f(x) | ﹣ | 0 | 2 | 0 | ﹣2 | ﹣ |
作图:
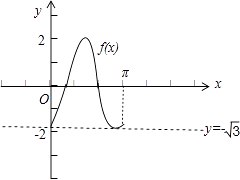
(2)解:令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ,可得函数的增区间为[kπ﹣
,可得函数的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
再结合x∈[﹣π,0],可得求f(x)=2sin(2x﹣ ![]() ),x∈[﹣π,0]的单调增区间为
),x∈[﹣π,0]的单调增区间为 ![]()
(3)解:把函数g(x)=2cos2x=2sin(2x+ ![]() )=2sin2(x+
)=2sin2(x+ ![]() ) 的图象向右平移
) 的图象向右平移 ![]() 个单位,就可得到f(x)=2sin2(x﹣
个单位,就可得到f(x)=2sin2(x﹣ ![]() )=2sin(2x﹣
)=2sin(2x﹣ ![]() )的图象
)的图象
【解析】(1)利用五点法做函数y=Asin(ωx+φ)的在一个周期[0,π]上的图象.(2)利用正弦函数的单调性求得f(x)在x∈[﹣π,0]的单调增区间.(3)利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为![]() ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
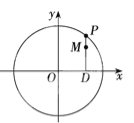
【题目】如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=![]() |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 18 | 7 | 25 |
女 | 12 | 13 | 25 |
合计 | 30 | 20 | 50 |
(1)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序,在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(2)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子,现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,下顶点为
,下顶点为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且三角形
,且三角形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相切,过焦点
相切,过焦点![]() ,
, ![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin2(2x﹣ ![]() )﹣2tsin(2x﹣
)﹣2tsin(2x﹣ ![]() )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ ![]() ,
, ![]() ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ![]() ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级学生会有理科生4名,其中3名男同学;文科生3名,其中有1名男同学.从这7名成员中随机抽4人参加高中示范校验收活动问卷调查.
(Ⅰ)设![]() 为事件“选出的4人中既有文科生又有理科生”,求事件
为事件“选出的4人中既有文科生又有理科生”,求事件![]() 的概率;
的概率;
(Ⅱ)设![]() 为选出的4人中男生人数与女生人数差的绝对值,求随机变量
为选出的4人中男生人数与女生人数差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设双曲线![]() 的上焦点为
的上焦点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为双曲线虚轴的左端点,已知
为双曲线虚轴的左端点,已知![]() 的离心率为
的离心率为![]() ,且
,且![]() 的面积
的面积![]() .
.

(1)求双曲线![]() 的方程;
的方程;
(2)设抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() ,动直线
,动直线![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的准线相交于点
的准线相交于点![]() ,试推断以线段
,试推断以线段![]() 为直径的圆是否恒经过
为直径的圆是否恒经过![]() 轴上的某个定点
轴上的某个定点![]() ?若是,求出定点
?若是,求出定点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com