
【题目】已知![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 且
且![]() ,
,![]() ,数列
,数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设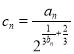 ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)证明:对一切![]() ,
,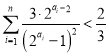
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)当![]() 时,构造
时,构造![]() ,变形为
,变形为![]() ,再求数列的通项公式;
,再求数列的通项公式;
(2)由已知变形为![]() ,利用累加法求数列
,利用累加法求数列![]() 的通项公式,然后再求数列
的通项公式,然后再求数列![]() 的通项公式,利用错位相减法求和;
的通项公式,利用错位相减法求和;
(3)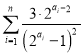 表示求数列
表示求数列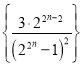 的前
的前![]() 项和,然后将通项放缩为
项和,然后将通项放缩为![]() 时,
时,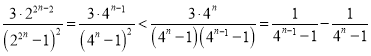 ,然后利用裂项相消法求和.
,然后利用裂项相消法求和.
(1)![]() 时,可得
时,可得![]() ,
,
![]() 时,
时,![]() ,
,![]() ,两式相减,
,两式相减,
得![]() ,
,![]() ,
,
![]() ,
,
![]() 数列
数列![]() 的奇数项和偶数项分别成以4为公差的等差数列,
的奇数项和偶数项分别成以4为公差的等差数列,
当![]() ,
,![]() 时,
时,![]() ,
,
当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,![]() .
.
(2)![]()
![]() ,
,
![]() ,即
,即![]() ,
,
整理为:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…………………………,
![]() ,
,![]() 时,
时,
这![]() 个式子相加可得
个式子相加可得![]() ,
,
![]() ,当
,当![]() 时,
时,![]() 成立,
成立,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
两式相减可得:![]()
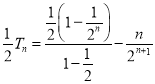 ,
,
![]()
(3)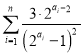 表示求数列
表示求数列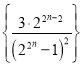 的前
的前![]() 项和,设前
项和,设前![]() 项和为
项和为![]() ,
,
当![]() 时,
时,![]() 成立,
成立,
当![]() 时,
时,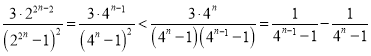
![]()
![]() .
.
综上可知![]() ,
,
![]() 对一切
对一切![]() ,
,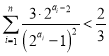 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年森林城市建设座谈会在深圳举行.会上宣读了国家森林城市称号批准决定,并举行授牌仪式,滕州市榜上有名,被正式批准为“国家森林城市”.为进一步推进国家森林城市建设,我市准备制定生态环境改造投资方案,该方案要求同时具备下列两个条件:
①每年用于风景区改造的费用![]() 随每年改造生态环境总费用
随每年改造生态环境总费用![]() 增加而增加;②每年用于风景区改造的费用
增加而增加;②每年用于风景区改造的费用![]() 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用![]() 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用![]() 的25%.若每年改造生态环境的总费用至少1亿元,至多4亿元;请你分析能否采用函数模型
的25%.若每年改造生态环境的总费用至少1亿元,至多4亿元;请你分析能否采用函数模型![]() 作为生态环境改造投资方案.
作为生态环境改造投资方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 平面ABC,平面
平面ABC,平面![]() 平面ABC,
平面ABC,![]() ,且
,且![]() .
.
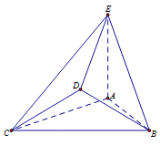
(1)若![]() ,求证:
,求证:![]() 平面BDE;
平面BDE;
(2)若二面角![]() 为
为![]() ,求直线CD与平面BDE所成角.
,求直线CD与平面BDE所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的焦点在
的焦点在![]() 轴上,点
轴上,点![]() 为坐标原点,射线
为坐标原点,射线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() 、点
、点![]() ,且
,且![]() ,试判断直线
,试判断直线![]() 与圆
与圆![]() :
:![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com