
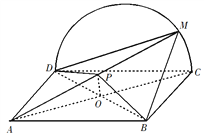
【题目】如图,矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.

【答案】(1)证明见解析
(2)存在,理由见解析
【解析】分析:(1)先证![]() ,再证
,再证![]() ,进而完成证明。
,进而完成证明。
(2)判断出P为AM中点,,证明MC∥OP,然后进行证明即可。
详解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC![]() 平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为![]() 上异于C,D的点,且DC为直径,所以DM⊥CM.
上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM![]() 平面AMD,故平面AMD⊥平面BMC.
平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC![]() 平面PBD,OP
平面PBD,OP![]() 平面PBD,所以MC∥平面PBD.
平面PBD,所以MC∥平面PBD.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a,b,定义运算“*”:a*b=![]() ,设f (x)=(x-4)*
,设f (x)=(x-4)*![]() ,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市现有人口总数为100万人,如果年自然增长率为![]() 试回答下面的问题:
试回答下面的问题:
(1)写出该城市人口总数![]() (万人)与年份
(万人)与年份![]() (年)的函数关系式;
(年)的函数关系式;
(2)计算10年以后该城市人口总数(精确度为0.1万人);
(3)计算大约多少年以后该城市人口总数将达到120万人(精确度为1年).
(提示:![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com