练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,表示以AB=4 cm,BC=3 cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5 cm,BF=8 cm,CG=12 cm时,试回答下列问题:

    (1)求DH的长;

    (2)求这个几何体的体积;

    (3)截面四边形EFGH是什么图形?并证明你的结论.

    解:(1)过E作EB1⊥BF,则BB1=AE=5,所以B1F=8-5=3.

    根据面面平行的定理,因为平面ABFE∥平面DCGH,EF和HG是它们分别与截面的交线,所以EF∥HG.

    过H作HC1⊥CG,垂足为C1.则

    GC1=FB1=3 cm,DH=12-3=9(cm).

    (2)用一个与该几何体完全相同的几何体,倒置其上,使它们拼接组合成一个以ABCD为底,高为17 cm的长方体.设原几何体的体积为V.所以

    2V=3×4×17=204(cm3),

    即V=102 cm3.

    (3)已知EF∥HG,同理,EH∥FG.

    于是EFGH是平行四边形.

    因为EF==5,过E作ED1⊥DH,则

    DD1=AE=5,ED1=AD=3,HD1=9-5=4,

    所以EH==5.

    所以EF=EH.故EFGH是菱形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    15、如图是表示以AB=4，BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体，其中四边形EFGH为截面．已知AE=5，BF=8，CG=12．
    （1）作出截面EFGH与底面ABCD的交线l；
    （2）截面四边形EFGH是否为菱形？并证明你的结论；
    （3）求DH的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
    A．（不等式选做题）不等式|
    x+1
    x-1
    |≥1    的解集是
    （-∞，0]
    （-∞，0]
    ．
    B．（几何证明选做题） 如图，以AB=4为直径的圆与△ABC的两边分别交于E，F两点，∠ACB=60°，则EF=
    2
    2
    ．
    C．（坐标系与参数方程选做题） 在极坐标中，已知点P为方程ρ（cosθ+sinθ）=1所表示的曲线上一动点，Q（2，
    π
    3
    ），则|PQ|的最小值为
    		6
    2
    		6
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省西安市西工大附中高考数学一模试卷（文科）（解析版） 题型：填空题

    （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
    A．（不等式选做题）不等式的解集是    ．
    B．（几何证明选做题） 如图，以AB=4为直径的圆与△ABC的两边分别交于E，F两点，∠ACB=60°，则EF=    ．
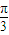    C．（坐标系与参数方程选做题） 在极坐标中，已知点P为方程ρ（cosθ+sinθ）=1所表示的曲线上一动点，Q（2，），则|PQ|的最小值为    ．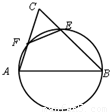

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省西安市西工大附中高考数学一模试卷（理科）（解析版） 题型：填空题

    （考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
    A．（不等式选做题）不等式的解集是    ．
    B．（几何证明选做题） 如图，以AB=4为直径的圆与△ABC的两边分别交于E，F两点，∠ACB=60°，则EF=    ．
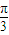    C．（坐标系与参数方程选做题） 在极坐标中，已知点P为方程ρ（cosθ+sinθ）=1所表示的曲线上一动点，Q（2，），则|PQ|的最小值为    ．

    查看答案和解析>>

    同步练习册答案