Question

【题目】某校进行了一次创新作文大赛，共有100名同学参赛，经过评判，这100名参赛者的得分都在之间，其得分的频率分布直方图如图，则下列结论错误的是

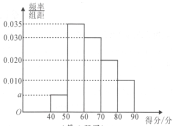
A. 得分在之间的共有40人

B. 从这100名参赛者中随机选取1人，其得分在的概率为

C. 这100名参赛者得分的中位数为65

D. 估计得分的众数为55

Answer 1

【答案】C

【解析】

根据频率分布直方图，利用最高的小矩形对应的底边中点估计众数；根据频率和为1，计算a的值；计算得分在[60，80）内的频率，用频率估计概率即可．

根据频率和为1，计算（a+0.035+0.030+0.020+0.010）×10=1，解得a=0.005，

得分在的频率是0.40，估计得分在的有100×0.40=40人，A正确；

得分在的频率为0.5，用频率估计概率，
知这100名男生中随机抽取一人，得分在的概率为，B正确．

根据频率分布直方图知，最高的小矩形对应的底边中点为 ，∴估计众数为55，D正确；

故选C.