
【题目】如图,岛 ![]() 、
、 ![]() 相距
相距 ![]() 海里.上午9点整有一客轮在岛
海里.上午9点整有一客轮在岛 ![]() 的北偏西
的北偏西 ![]() 且距岛
且距岛 ![]()
![]() 海里的
海里的 ![]() 处,沿直线方向匀速开往岛
处,沿直线方向匀速开往岛 ![]() ,在岛
,在岛 ![]() 停留
停留 ![]() 分钟后前往
分钟后前往 ![]() 市.上午
市.上午 ![]() 测得客轮位于岛
测得客轮位于岛 ![]() 的北偏西
的北偏西 ![]() 且距岛
且距岛 ![]()
![]() 海里的
海里的 ![]() 处,此时小张从岛
处,此时小张从岛 ![]() 乘坐速度为
乘坐速度为 ![]() 海里/小时的小艇沿直线方向前往
海里/小时的小艇沿直线方向前往 ![]() 岛换乘客轮去
岛换乘客轮去 ![]() 市.
市.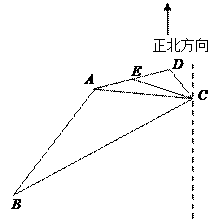
(Ⅰ)若 ![]() ,问小张能否乘上这班客轮?
,问小张能否乘上这班客轮?
(Ⅱ)现测得 ![]() ,
, ![]() .已知速度为
.已知速度为 ![]() 海里/小时(
海里/小时( ![]() )的小艇每小时的总费用为(
)的小艇每小时的总费用为( ![]() )元,若小张由岛
)元,若小张由岛 ![]() 直接乘小艇去
直接乘小艇去 ![]() 市,则至少需要多少费用?
市,则至少需要多少费用?
【答案】解:(Ⅰ)根据题意得:![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
在 ![]() 中,由余弦定理得,
中,由余弦定理得,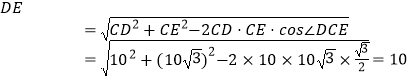 ,
,
所以客轮的航行速度 ![]() (海里/小时).
(海里/小时).
因为 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() .
.
在 ![]() 中,由余弦定理得,
中,由余弦定理得, ![]() ,
,
整理得: ![]() ,
,
解得 ![]() 或
或 ![]() (不合舍去).
(不合舍去).
所以客轮从 ![]() 处到岛
处到岛 ![]() 所用的时间
所用的时间 ![]() 小时,
小时,
小张到岛 ![]() 所用的时间至少为
所用的时间至少为 ![]() 小时.
小时.
由于 ![]() ,
,
所以若小张9点半出发,则无法乘上这班客轮.
(Ⅱ)在 ![]() 中,
中, ![]() ,
, ![]() ,
,
所以 ![]() 为锐角,
为锐角, ![]() ,
, ![]() .
.
所以 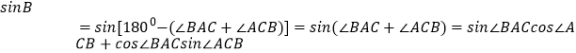
![]() .
.
由正弦定理得, ![]() ,
,
所以 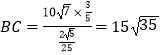 ,
,
所以小张由岛 ![]() 直接乘小艇去城市
直接乘小艇去城市 ![]() 的总费用为
的总费用为![]() (
( ![]() ),
),
当且仅当 ![]() ,即
,即 ![]() 时,
时, ![]() (元).
(元).
所以若小张由岛 ![]() 直接乘小艇去
直接乘小艇去 ![]() 市,其费用至少需
市,其费用至少需 ![]() 元
元
【解析】(Ⅰ)根据题目中所给的条件的特点,在△CDE中,由余弦定理得DE.在△ACE中,由余弦定理得AE,最后求出客轮从E处到岛A所用的时间,小张到岛A所用的时间.即可推出正确的答案.
(Ⅱ)求出BC,利用基本不等式求出最值即可.考查正弦定理、余弦定理及三角恒等变换等基础知识.


科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“a>0,b>0”是“ ![]() ≥2”的充要条件
≥2”的充要条件
C.命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1或x≠2,则x2-3x+2≠0”
D.命题p:x∈R,x2+x-1<0,则﹁p:x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的函数f(x)满足f(x+2)=-f(x),且  ,则函数g(x)=lg x的图象与函数f(x)的图象的交点个数为( )
,则函数g(x)=lg x的图象与函数f(x)的图象的交点个数为( )
A.3
B.5
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非零平面向量 ![]() ,
, ![]() ,则“|
,则“| ![]() |=|
|=| ![]() |+|
|+| ![]() |”是“存在非零实数λ,使
|”是“存在非零实数λ,使 ![]() =λ
=λ ![]() ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从甲、乙两个品牌共9个不同的空气净化器中选出3个分别测试A、B、C三项指标,若取出的3个空气净化器中既有甲品牌又有乙品牌的概率为 ![]() ,那么9个空气净化器中甲、乙品牌个数分布可能是( )
,那么9个空气净化器中甲、乙品牌个数分布可能是( )
A.甲品牌1个,乙品牌8个
B.甲品牌2个,乙品牌7个
C.甲品牌3个,乙品牌6个
D.甲品牌4个,乙品牌5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A.若 ![]() 的观测值为
的观测值为 ![]() ,在犯错误的概率不超过
,在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
B.由独立性检验可知,在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有
的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有 ![]() 的可能患有肺癌.
的可能患有肺癌.
C.若从统计量中求出在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系,是指有
的前提下认为吸烟与患肺癌有关系,是指有 ![]() 的可能性使得判断出现错误.
的可能性使得判断出现错误.
D.以上三种说法都不正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是双曲线 ![]() 的右顶点,F(c,0)是右焦点,若抛物线
的右顶点,F(c,0)是右焦点,若抛物线 ![]() 的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
A.[2,+∞)
B.(1,2]
C.(1,3]
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计 ![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数 ![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生 ![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为 ![]() ,则由此可估计
,则由此可估计 ![]() 的近似值为( )
的近似值为( )
A.3.119
B.3.124
C.3.132
D.3.151
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com