
分析 (1)由题意得,利用an与Sn的关系求出{an}的通项公式,单独求出n=1时a1的值,验证其是否满足通项公式,即可求出{an}的通项公式;利用等比数列的性质将{bn}的公比求出,即可求出其通项公式;
(2)由(1)中求出的{an}和{bn}的通项公式代入新数列中,写出新数列的通项公式,利用错位相减法求出其前n项和Tn.
解答 解:由题意得:
(1)因为Sn=2n2+n①,所以Sn-1=2(n-1)2+(n-1)②,
所以①-②得:an=Sn-Sn-1=4n-1(n≥2);
当n=1时,a1=S1=3;
所以an=4n-1,n∈N*,
又因为等比数列{bn}满足b1=1,b4=8,n∈N*,
所以${q}^{3}=\frac{{b}_{4}}{{b}_{1}}$=8,
所以q=2,
所以bn=2n-1;
(2)由(1)可知an•bn=(4n-1)2n-1,
所以Tn=3+7×21+11×22+…+(4n-5)×2n-2+(4n-1)×2n-1①,
2Tn=3×2+7×22+11×23+…+(4n-5)×2n-1+(4n-1)×2n②,
所以①-②得:-Tn=3+4×2+4×22+4×23+…+4×2n-1-(4n-1)×2n②,
Tn=5+(4n-5)×2n.
点评 (1)本题难度中档,解题关键在于对an=Sn-Sn-1的关系熟练掌握,以及等比数列相关知识点的掌握;(2)难度中上,解题关键在于对错位相减法求数列前n项和的方法的掌握和应用.


科目:高中数学 来源: 题型:解答题
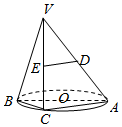 AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}$ | C. | $\root{4e}{e}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
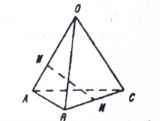
如图,空间四边形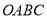 中,
中,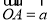 ,
,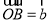 ,
,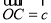 ,点
,点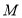 在
在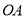 上,且
上,且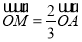 ,点
,点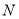 为
为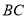 中点,则
中点,则 等于( )
等于( )
A.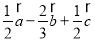 B.
B.
C.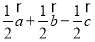 D.
D.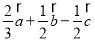
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com