
【题目】如图所示,在正三棱柱ABCA1B1C1中,AB=2,AA1=2,由顶点B沿棱柱侧面(经过棱AA1)到达顶点C1,与AA1的交点记为M.求:
(1)三棱柱侧面展开图的对角线长;
(2)从B经M到C1的最短路线长及此时![]() 的值.
的值.

【答案】(1) ![]() .
.
(2)![]() 1.
1.
【解析】
(1)正三棱柱ABC﹣A1B1C1的侧面展开图是长为6,宽为2的矩形,直接可以求出对角线长;
(2)将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线,求出DC1和![]() 的值即可;
的值即可;
沿侧棱BB1将正三棱柱的侧面展开,得到一个矩形BB1B′1B′(如下图).
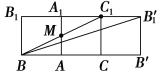
(1)矩形BB1B′1B′的长BB′=6,宽BB1=2.所以三棱柱侧面展开图的对角线长为![]() =2
=2![]() .
.
(2) 如图,将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点D的位置,连接DC1交AA1于M,则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线,其长为![]() ∵△DMA≌△C1MA1,∴AM=A1M,故
∵△DMA≌△C1MA1,∴AM=A1M,故![]()


科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形无底仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m,高4m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线Γ由曲线C1: ![]() (a>b>0,y≤0)和曲线C2:
(a>b>0,y≤0)和曲线C2: ![]() (a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(Ⅰ)若F2(2,0),F3(﹣6,0),求曲线Γ的方程;
(Ⅱ)如图,作直线l平行于曲线C2的渐近线,交曲线C1于点A、B,求证:弦AB的中点M必在曲线C2的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线Γ,若直线l1过点F4交曲线C1于点C、D,求△CDF1面积的最大值.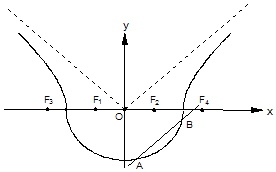
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是___________
![]() 用一个平面截一个球,得到的截面是一个圆;
用一个平面截一个球,得到的截面是一个圆;
![]() 圆台的任意两条母线延长后一定交于一点;
圆台的任意两条母线延长后一定交于一点;
![]() 有一个面为多边形,其余各面都是三角形的几何体叫做棱锥;
有一个面为多边形,其余各面都是三角形的几何体叫做棱锥;
![]() 若棱锥的侧棱长与底面多边形的边长相等,则该棱锥不可能是正六棱锥;
若棱锥的侧棱长与底面多边形的边长相等,则该棱锥不可能是正六棱锥;
![]() 用斜二测画法作出正三角形的直观图,则该直观图面积为原三角形面积的一半.
用斜二测画法作出正三角形的直观图,则该直观图面积为原三角形面积的一半.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
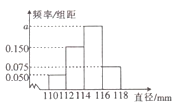
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年某学科能力测试共有12万考生参加,成绩采用15级分,测试成绩分布图如图,试估计成绩高于11级分的人数为 ( )

A. 8 000 B. 10 000 C. 20 000 D. 60 000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(x∈(0,2π))有两个不同的零点x1、x2 , 方程f(x)=m有两个不同的实根x3、x4 . 若把这四个数按从小到大排列构成等差数列,则实数m的值为( )
A.![]()
B.![]()
C.![]()
D.- ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com