
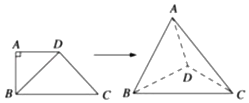
【题目】如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A﹣BCD,则在三棱锥A﹣BCD中,下列判断正确的是_____.(写出所有正确的序号)

①平面ABD⊥平面ABC
②直线BC与平面ABD所成角是45°
③平面ACD⊥平面ABC
④二面角C﹣AB﹣D余弦值为![]()
【答案】②③④
【解析】
①反证法,假设平面![]() 平面
平面![]() ,容易推出
,容易推出![]() 垂直于平面
垂直于平面![]() ,从而
,从而![]() ,出矛盾;
,出矛盾;
②利用几何法找到其平面角为![]() ,求解即可判断;
,求解即可判断;
③证明![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ;
;
④证明![]() 为二面角
为二面角![]() 的平面角,求解三角形得二面角的余弦值判断.
的平面角,求解三角形得二面角的余弦值判断.
在四边形ABCD中,由已知可得∠DBC=45°,假设平面ABD⊥平面ABC,
又平面ABD⊥平面BCD,且平面ABD∩平面BDC=BC,可得BC⊥平面ABD,
有∠DBC=90°,与∠DBC=45°矛盾,则假设错误,故①错误;
在四边形ABCD中,由已知可得BD⊥DC,
又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,则DC⊥平面ABD,
∠DBC为直线BC与平面ABD所成角是45°,故②正确;
由判断②时可知,DC⊥平面ABD,则DC⊥AB,又BA⊥AD,AD∩DC=D,则AB⊥平面ADC,
而AB平面ABC,则平面ACD⊥平面ABC,故③正确;
由判断③时可知,AB⊥平面ADC,则∠DAC为二面角C﹣AB﹣D的平面角,
设AD=AB=1,则BD=DC![]() ,由DC⊥AD,得AC
,由DC⊥AD,得AC![]() ,得cos∠DAC
,得cos∠DAC![]() ,故④正确.
,故④正确.
∴判断正确的是②③④.
故答案为:②③④.


科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于5的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C分别为△ABC的三边a,b,c所对的角,向量![]() =(sin A,sin B),
=(sin A,sin B),![]() =(cos B,cos A),且
=(cos B,cos A),且![]() =sin 2C.
=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差数列,且![]() ,求边c的长.
,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,下列结论正确的是( )
A.AC⊥BDB.△ACD是等边三角形
C.AB与平面BCD成![]() 角D.AB与CD所成的角是60°
角D.AB与CD所成的角是60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,所有棱长均相等,且AA1⊥平面ABC,点D、E、F分别为所在棱的中点.

(1)求证:EF∥平面CDB1;
(2)求异面直线EF与BC所成角的余弦值;
(3)求二面角B1﹣CD﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,D,E分别为AB,AC的中点,
中,D,E分别为AB,AC的中点,![]() ,以DE为折痕将
,以DE为折痕将![]() 折起,使点A到达点P的位置,如图.
折起,使点A到达点P的位置,如图.

(1)证明:![]() ;
;
(2)若平面DEP![]() 平面BCED,求直线DC与平面BCP所成角的正弦值。
平面BCED,求直线DC与平面BCP所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com