
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.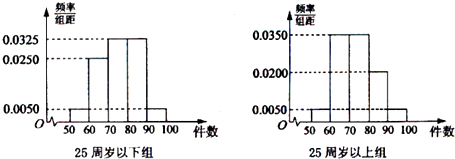
附表:
P(K2≥k) | 0.100 | 0.010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
K2= ![]() ,(其中n=a+b+c+d)
,(其中n=a+b+c+d)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | |||
25周岁以下组 | |||
合计 |
【答案】
(1)解:由已知可得,样本中有25周岁以上组工人100× ![]() =60名,
=60名,
25周岁以下组工人100× ![]() =40名,
=40名,
所以样本中日平均生产件数不足60件的工人中,25周岁以上组工人有60×0.05=3(人),
25周岁以下组工人有40×0.05=2(人),
故从中随机抽取2名工人所有可能的结果共 ![]() =10种,
=10种,
其中至少1名“25周岁以下组”工人的结果共 ![]()
![]() +
+ ![]() =7种,
=7种,
故所求的概率为: ![]() ;
;
(2)解:由频率分布直方图可知:在抽取的100名工人中,“25周岁以上组”中的生产能手有60×0.25=15(人),
“25周岁以下组”中的生产能手有40×0.375=15(人),据此可得2×2列联表如下:
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | 15 | 45 | 60 |
25周岁以下组 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
所以可得k2= ![]() ≈1.79,
≈1.79,
因为1.79<2.706,所以没有90%的把握认为“生产能手与工人所在的年龄组有关”
【解析】(1)由分层抽样的特点可得样本中有25周岁以上、下组工人人数,再由所对应的频率可得样本中日平均生产件数不足60件的工人中,25周岁以上、下组工人的人数分别为3,2,由古典概型的概率公式可得答案;(2)由频率分布直方图可得“25周岁以上组”中的生产能手的人数,以及“25周岁以下组”中的生产能手的人数,据此可得2×2列联表,可得k2≈1.79,由1.79<2.706,可得结论.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3},N={1,2,3,4},定义函数f:M→N.若点A(1,f(1))、B(2,f(2))、C(3,f(3)),△ABC的外接圆圆心为D,且 ![]() ,则满足条件的函数f(x)有( )
,则满足条件的函数f(x)有( )
A.6个
B.10个
C.12个
D.16个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,3)B(3,1),C(﹣1,0)求:
(1)求BC及BC边上的中线所在直线的方程;
(2)求BC边上的垂直平分线所在直线方程;
(3)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com