Question

【题目】如图，在四棱锥中，四边形为正方形，面，且，为中点．

（1）证明：//平面；

（2）证明：平面平面；

（3）求二面角的余弦值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）连接BD与AC交于点O，连接EO，证明EO//PB，由线线平行证明线面平行即可；（2）通过证明CD平面PAD来证明平面平面；（3）以A为坐标原点，所在直线分别为x轴，y轴，z轴建立空间直角坐标系，通过空间向量的方法求二面角的余弦值.

（1）证明：连结BD交AC于点O，连结EO．

O为BD中点，E为PD中点，

∴EO//PB．

EO平面AEC，PB平面AEC，

∴ PB//平面AEC．

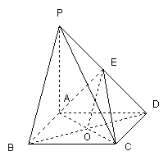
（2）证明：PA⊥平面ABCD．平面ABCD，

∴．

又在正方形ABCD中且，

∴CD平面PAD．

又平面PCD，

∴平面平面．

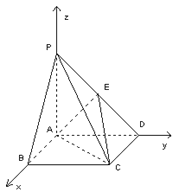
（3）如图，以A为坐标原点，所在直线分别为x轴，y轴，z轴建立空间直角坐标系．

由PA=AB=2可知A、B、C、D、P、E的坐标分别为

A（0, 0, 0）, B（2, 0, 0）,C（2, 2, 0）,

D（0, 2, 0）, P（0, 0, 2）, E（0, 1, 1） ．

PA平面ABCD，∴是平面ABCD的法向量，=（0, 0, 2）．

设平面AEC的法向量为,, ,

则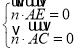,即

∴令 ,则.

∴,

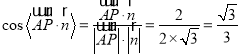二面角的余弦值为