
| A. | $\frac{1}{100}$ | B. | $\frac{1}{121}$ | C. | $\frac{99}{100}$ | D. | $\frac{120}{121}$ |
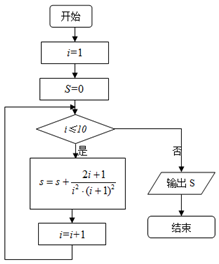
分析 模拟执行程序框图,可得程序框图的功能是计算并输出S=$\frac{3}{1×{2}^{2}}$+$\frac{5}{{2}^{2}×{3}^{2}}$+$\frac{7}{{3}^{2}×{4}^{2}}$+…+$\frac{21}{1{0}^{2}×1{1}^{2}}$的值,由裂项法即可计算得解.
解答 解:模拟执行程序框图,可得程序框图的功能是计算并输出S=$\frac{3}{1×{2}^{2}}$+$\frac{5}{{2}^{2}×{3}^{2}}$+$\frac{7}{{3}^{2}×{4}^{2}}$+…+$\frac{21}{1{0}^{2}×1{1}^{2}}$的值,
由于:$\frac{2i+1}{{i}^{2}•(i+1)^{2}}$=$\frac{i+(i+1)}{{i}^{2}•(i+1)^{2}}$=$\frac{1}{i(i+1)}$($\frac{1}{i}$+$\frac{1}{i+1}$)=($\frac{1}{i}$-$\frac{1}{i+1}$)($\frac{1}{i}$+$\frac{1}{i+1}$)=$\frac{1}{{i}^{2}}$-$\frac{1}{(i+1)^{2}}$,
所以:S=$\frac{3}{1×{2}^{2}}$+$\frac{5}{{2}^{2}×{3}^{2}}$+$\frac{7}{{3}^{2}×{4}^{2}}$+…+$\frac{21}{1{0}^{2}×1{1}^{2}}$
=($\frac{1}{{1}^{2}}$-$\frac{1}{{2}^{2}}$)+($\frac{1}{{2}^{2}}$-$\frac{1}{{3}^{2}}$)+…+($\frac{1}{1{0}^{2}}$-$\frac{1}{1{1}^{2}}$)
=$\frac{1}{{1}^{2}}$-$\frac{1}{1{1}^{2}}$
=$\frac{120}{121}$.
故选:D.
点评 本题主要考查了循环结构的程序框图,考查了裂项法求数列的和,属于基础题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
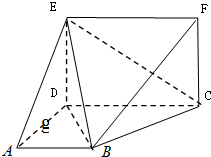 如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.
如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=10 n=20 n=m m=n | |
| B. | m=10 n=20 s=m n=s | |
| C. | m=10 n=20 s=m m=n n=s | |
| D. | m=10 n=20 s=m t=n n=s m=n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
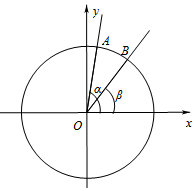 如图,在平面直角坐标系xOy中,以O为顶点,x轴的非负半轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为$\frac{\sqrt{2}}{10},\frac{3}{5}$.
如图,在平面直角坐标系xOy中,以O为顶点,x轴的非负半轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知A,B的横坐标分别为$\frac{\sqrt{2}}{10},\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
如图,网格纸上正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )| A. | $\frac{13}{3}$ | B. | $\frac{14}{3}$ | C. | $\frac{15}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com