
分析 (1)首先根据向量的坐标运算求出函数的解析式,进一步变函数为正弦型函数,最后求出单调区间.
(2)根据函数与的定义域求出函数的值域,进一步利用恒成立问题,求出k的取值范围
解答 解:由已知f(x)=2$\overrightarrow{a}$•$\overrightarrow{b}$+1=2(cos2x+$\sqrt{3}$sinxcosx)+1=cos2x+$\sqrt{3}$sin2x+2=2sin(2x+$\frac{π}{6}$)+2;
所以(1)当$x∈[0,\frac{π}{2}]$时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],sin(2x+$\frac{π}{6}$)∈[$-\frac{1}{2}$,1],所以f(x)的值域[1,4];
(2)对任意$x∈[0,\frac{π}{2}]$和任意$α∈[\frac{π}{12},\frac{π}{3}]$,$k•\sqrt{1+sin2α}-sin2α≤f(x)+1$恒成立,
即k|sinα+cosα|-sin2α≤f(x)+1恒成立,又f(x)+1的最小值为2,
所以只要k|sinα+cosα|≤2+sin2α,
所以k≤|sinα+cosα|+$\frac{1}{|sinα+cosα|}$,又$α∈[\frac{π}{12},\frac{π}{3}]$,
所以|sinα+cosα|∈[$\frac{\sqrt{6}}{2}$,$\sqrt{2}$],
|sinα+cosα|+$\frac{1}{|sinα+cosα|}$∈[$\frac{5\sqrt{6}}{6}$,$\frac{3\sqrt{2}}{2}$]
所以k≤$\frac{5\sqrt{6}}{6}$.
点评 本题考查的知识要点:三角函数关系式的恒等变换,向量的坐标运算,正弦型函数的值域,恒成立问题的应用,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 3020 | D. | 3021 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单位编号x | 1 | 2 | 3 | 4 | 5 |
| 投资额y | 3.3 | 3.6 | 3.9 | 4.4 | 4.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
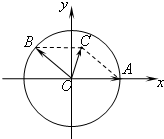 如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com