练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题12分）设有关于的一元二次方程．

    （1）若是从0，1，2，3四个数中任取的一个数，是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．

    （2）若是从区间任取的一个数，是从区间任取的一个数，求上述方程有实根的概率．

     

     

    【答案】

    解：设事件为“方程有实根”．

    当，时，方程有实根的充要条件为．…………2分

    （Ⅰ）基本事件共12个：

    ．其中第一个数表示的取值，第二个数表示的取值．

    事件中包含9个基本事件，事件发生的概率为．…………6分

    （Ⅱ）试验的全部结束所构成的区域为．

    构成事件的区域为．

    所以所求的概率为．………………12分

     

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东省枣庄市2010届高三年级调研考试数学（文科）试题 题型：解答题

    （本题满分12分）
    如图，斜率为1的直线过抛物线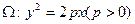的焦点F，与抛物线交于两点A，B。
    （1）若|AB|=8，求抛物线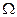的方程；
    （2）设C为抛物线弧AB上的动点（不包括A，B两点），求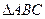的面积S的最大值；
    （3）设P是抛物线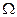上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）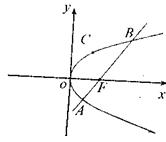

    查看答案和解析>>

    科目：高中数学 来源：2012届广西桂林中学高三7月月考试题理科数学 题型：解答题

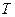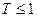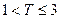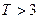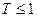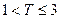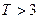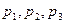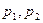    （本题满分12分）某种家用电器每台的销售利润与该电器的无故障使用时间（单位：年）有关. 若，则销售利润为0元；若，则销售利润为100元；若，则销售利润为200元. 设每台该种电器的无故障使用时间，及这三种情况发生的概率分别为，又知是方程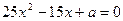的两个根，且.
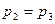    （Ⅰ）求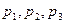的值；
    （Ⅱ）记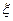表示销售两台这种家用电器的销售利润总和，求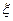的分布列和期望。

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广西桂林中学高三7月月考试题理科数学 题型：解答题

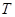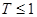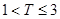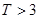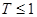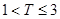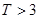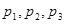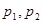    （本题满分12分）某种家用电器每台的销售利润与该电器的无故障使用时间（单位：年）有关. 若，则销售利润为0元；若，则销售利润为100元；若，则销售利润为200元. 设每台该种电器的无故障使用时间，及这三种情况发生的概率分别为，又知是方程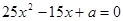的两个根，且.

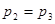    （Ⅰ）求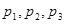的值；

    （Ⅱ）记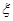表示销售两台这种家用电器的销售利润总和，求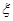的分布列和期望。

     

     

    查看答案和解析>>

    科目：高中数学 来源：山东省枣庄市2010届高三年级调研考试数学（文科）试题 题型：解答题

    （本题满分12分）

    如图，斜率为1的直线过抛物线的焦点F，与抛物线交于两点A，B。

       （1）若|AB|=8，求抛物线的方程；

       （2）设C为抛物线弧AB上的动点（不包括A，B两点），求的面积S的最大值；

       （3）设P是抛物线上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）

     

    查看答案和解析>>

    科目：高中数学 来源：2010年江西省高三热身卷数学（理）试题 题型：解答题

    （本题12分）某种家电器每台的销售利润与该电器无故障使用时间T（单位：年）有关，若T≤1，则销售利润为0元，若1＜T≤3，则销售利润为100元，若T＞3，则销售利润为200元，设每台该种电台无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率为为P1，P2，P3，又知P1，P2是方程25x2－15x＋a＝0的两个根，且P2＝P3，

    （1）求P1，P2，P3的值；

    （2）记表示销售两台这种家用电器的销售利润总和，求的分布列；

    （3）求销售两台这种家用电器的销售利润总和的平均值。

     

    查看答案和解析>>

    同步练习册答案