
(本小题满分12分)
已知函数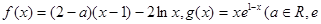 为自然对数的底数).
为自然对数的底数).
当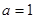 时,求
时,求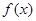 的单调区间;若函数
的单调区间;若函数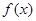 在
在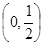 上无零点,求
上无零点,求 最小值;
最小值;
若对任意给定的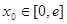 ,在
,在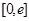 上总存在两个不同的
上总存在两个不同的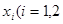 ),使
),使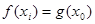 成立,求
成立,求 的取值范围.
的取值范围.
(1) 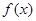 的单调递减区间为(0,2),单调递增区间为(2,
的单调递减区间为(0,2),单调递增区间为(2, ).
).
(2)  的最小值为
的最小值为 .
.
(3) 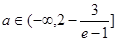 时,对任意给定的
时,对任意给定的 ,在
,在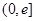 上总存在两个不同的
上总存在两个不同的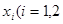 ),使得
),使得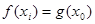 成立。
成立。
解析试题分析:解:(I)当
科目:高中数学
来源:
题型:解答题
有三张正面分别写有数字—2,—1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值。放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y)。
科目:高中数学
来源:
题型:解答题
(本小题共8分)
科目:高中数学
来源:
题型:解答题
(本小题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 时,
时,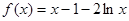 ,则
,则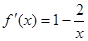 .由
.由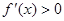 得
得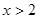 ;由
;由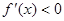 得
得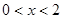 .故
.故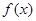 的单调递减区间为(0,2),单调递增区间为(2,
的单调递减区间为(0,2),单调递增区间为(2,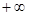 ).
).
(II)因为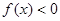 在区间
在区间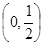 上恒成立是不可能的,故要使函数
上恒成立是不可能的,故要使函数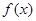 在
在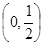 上无零点,只要对任意
上无零点,只要对任意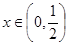 ,
,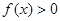 恒成立.即对
恒成立.即对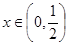 ,
,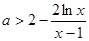 恒成立.令
恒成立.令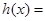
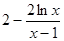 ,
,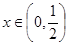 ,则
,则 ,再令
,再令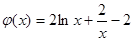 ,
,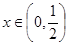 ,则
,则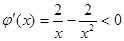 。故
。故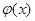 在
在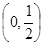 为减函数,于是
为减函数,于是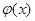
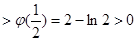 ,从而
,从而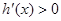 ,于是
,于是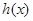 在
在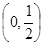 上为增函数,所以
上为增函数,所以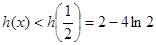 ,故要使
,故要使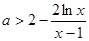 恒成立,只要
恒成立,只要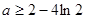 .综上可知,若函数
.综上可知,若函数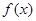 在
在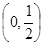 上无零点,则
上无零点,则 的最小值为
的最小值为 .
.
(III)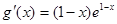 ,所以
,所以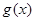 在
在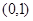 上递增,在
上递增,在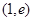 上递减.又
上递减.又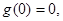
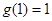 ,
,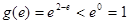 ,所以函数
,所以函数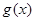 在
在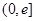 上的值域为
上的值域为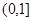 .当
.当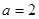 时,不合题意;当
时,不合题意;当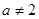 时,
时,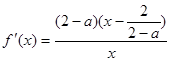 ,
, 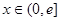 。
。
当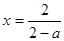 时,
时,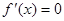 ,由题意知,
,由题意知,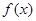 在
在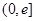 上不单调,故
上不单调,故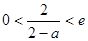 ,即
,即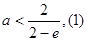 。此时,当
。此时,当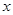 变化时,
变化时,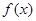 ,
,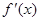 的变化情况如下:
的变化情况如下: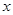
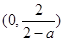
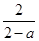


超能学典江苏13大市中考试卷分类汇编系列答案
经纶学典江苏13大市中考试卷汇编四色卷系列答案
金榜之路中考总复习中考全真模拟封闭卷系列答案
亮点激活高分宝典系列答案
天利38套对接高考单元专题训练系列答案
最新3年中考利剑中考试卷汇编系列答案
考进名校系列答案
北京市重点城区3年真题2年模拟试卷系列答案
河南省重点中学模拟试卷精选及详解系列答案
成都中考真题精选系列答案
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简分式 ;并求使分式的值为整数的(x,y)出现的概率。
;并求使分式的值为整数的(x,y)出现的概率。
已知函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y),且当x>0时,f(x)>0,f(-1)=-2,求f(x)在[-2,1]上的值域。
已知定义在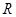 上的函数
上的函数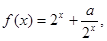
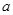 为常数,若
为常数,若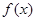 为偶函数,
为偶函数,
(1)求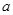 的值;
的值;
(2)判断函数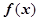 在
在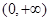 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;
(3)求函数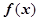 的值域.
的值域.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号