
【题目】已知圆![]() .
.
(1)求圆心C的坐标及半径r的大小;
(2)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程;
(3)从圆外一点![]() 向圆引一条切线,切点为M,O为坐标原点,且
向圆引一条切线,切点为M,O为坐标原点,且![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆上异于A、B的点,PO垂直于圆O所在的平面,且PO=OB![]() ,BC=2,点E在线段PB上,则CE+OE的最小值为_____.
,BC=2,点E在线段PB上,则CE+OE的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
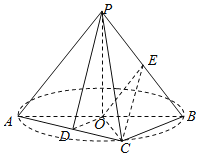
【题目】如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC, PD⊥PB,AD=1,BC=3,CD=4,PD=2.

(1)求异面直线AP与BC所成角的余弦值.
(2)求直线AB与平面PBC所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,对称轴为坐标轴,椭圆
的中心在原点,对称轴为坐标轴,椭圆![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点(
两点(![]() ,
, ![]() 不是长轴端点),且以
不是长轴端点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() , _______,求
, _______,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
①![]() ,
,![]() ,且
,且![]() ;
;
②![]() ;
;
③![]() ,
,![]() .
.
注:这三个条件中选一个,补充在上面的问题中并对其进行求解,如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表中的数表为“森德拉姆筛”(森德拉姆,东印度学者),其特点是每行每列都成等差数列.
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
在上表中,2017出现的次数为( )
A. 18 B. 36 C. 48![]() D. 72
D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,过
,过![]() 且与
且与![]() 轴垂直的直线与椭圆
轴垂直的直线与椭圆![]() 在第一象限内的交点为
在第一象限内的交点为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com