解:(1)由f(x)=2x
3+3(1-2a)x+6a(a-1)x求导数得到f'(x)=6x
2+6(1-2a)x+6a(a-1)
=6(x-a)(x-a+1)
∴y=f(x)在(-∞,a-1]上为增函数;
在[a-1,a]上为减函数;在[a,+∞)上为增函数.…
(2)由f(x)=x[2x
2+3(1-2a)x+6a(a-1)]
对于关于x的二次方程2x
2+3(1-2a)x+6a(a-1)=0无实根或仅有零根,仅有零根不可能则判别式△=[3(1-2a)]
2-4•2•6a(a-1)
=3(-2a+3)(2a+1)<0
∴
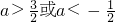
故所求a的范围为
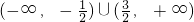
…
(3)设y=1与y=f(x)相切于点(x
0,y
0)
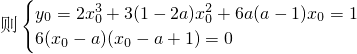
在x
0=a时,则2a
3+3(1-2a)a
2+6a
2(a-1)=1
∴
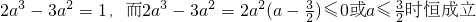
.
∴2a
3-3a
2=1不可能成立.
在x
0=a-1时,则2(a-1)
3+3(1-2a)(a-1)
2+6a(a-1)
2=1
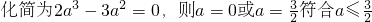
.
因此所求符合条件的a值分别为
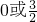
.…
分析:(1)先求函数的定义域,然后对函数求导可得f'(x)=6x
2+6(1-2a)x+6a(a-1),分别令f′(x)>0f′(x)<0可求函数的单调增区间,单调减区间;
(2)由于f(x)=x[2x
2+3(1-2a)x+6a(a-1)],所以关于x的方程f(x)=0有且仅有一个实数根等价于,对于关于x的二次方程2x
2+3(1-2a)x+6a(a-1)=0无实根或仅有零根,因为方程没有零根,所以二次方程2x
2+3(1-2a)x+6a(a-1)=0无实根,所以判别式<0,故可求a的范围;
(3)假设y=1与y=f(x)相切于点(x
0,y
0),则函数在极值点处与y=1相切,从而分类讨论:x
0=a及x
0=a-1,由此可得方程,故可求符合条件的a值.
点评:本题的考点是导数的应用,主要考查函数的单调性,导数的几何意义,考查方程根的判断,求函数的单调区间关键是先求函数的定义域,然后结合导数的符号进行求解,此类问题容易忽略对定义域的判断.利用导数的几何意义设出切点坐标是解决该问题的关键

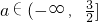 ,使得直线y=1与y=f(x)相切,如果存在,求出a,否则请说明理由.
,使得直线y=1与y=f(x)相切,如果存在,求出a,否则请说明理由.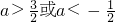
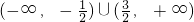 …
…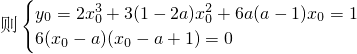
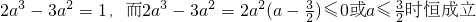 .
.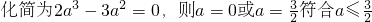 .
.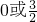 .…
.…

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案