
如图,已知三角形△ABC与△BCD所在平面相互垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
(Ⅰ)求证:AB⊥CQ;
(Ⅱ)求BP的长;
(Ⅲ)求直线AP与平面BCD所成的角.
(I)见解析;(Ⅱ)1;(Ⅲ)45°
解析试题分析:(I)由面ABC⊥面BCQ又CQ⊥BC推出CQ⊥面ABC,再推出CQ⊥AB;(Ⅱ)作AO⊥BC,垂足为O,则AO⊥平面BCQ,连接OP,由沿直线PQ将△PQD向上翻折,使D与A重合可知AP=DP即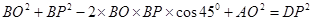 ,解得BP=1;(Ⅲ)由(Ⅱ)知AO⊥平面BCD,所以∠APO是直线AP与平面BCD所成的角,
,解得BP=1;(Ⅲ)由(Ⅱ)知AO⊥平面BCD,所以∠APO是直线AP与平面BCD所成的角, ,因此直线AP与平面BCD所成的角为45°.
,因此直线AP与平面BCD所成的角为45°.
试题解析:(I)证明:∵面ABC⊥面BCQ 又CQ⊥BC
∴CQ⊥面ABC
∴CQ⊥AB;
(Ⅱ)解:作AO⊥BC,垂足为O,则AO⊥平面BCQ,连接OP,
设AB=1,则BD=2,设BP=x,
由题意AP=DP,
∴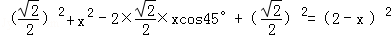 ,
,
∴x=1;
(Ⅲ)解:由(Ⅱ)知AO⊥平面BCD,
∴∠APO是直线AP与平面BCD所成的角,
∴∠APO=45°,
∴直线AP与平面BCD所成的角为45°.
考点:1.空间直线的位置关系的判定;2.空间两点间的距离;3.线面角的求解


科目:高中数学 来源: 题型:解答题
如图,ABCD是正方形,O是正方形的中心,PO 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE (4分)
(2)平面PAC 平面BDE(6分)
平面BDE(6分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
A是△BCD平面外的一点,E,F分别是BC,AD的中点.
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知平面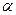 与
与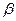 是两个不同的平面.下列条件中,能判定平面
是两个不同的平面.下列条件中,能判定平面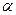 与
与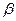 平行的条件可以
平行的条件可以
是 .(写出所有正确条件的序号)
①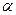 内有无穷多条直线都与
内有无穷多条直线都与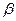 平行; ②
平行; ②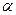 内的任何直线都与
内的任何直线都与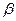 平行;
平行;
③直线a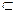
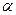 ,直线b
,直线b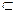
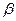 ,且a∥
,且a∥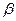 ,b∥
,b∥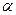 ; ④a⊥
; ④a⊥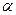 ,b⊥
,b⊥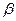 ,a∥b.
,a∥b.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知 、
、 、
、 是直线,
是直线,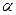 是平面,给出下列命题:①若
是平面,给出下列命题:①若 ,
, ,则
,则 ;
;
②若 ,
, ,则
,则 ;③若
;③若 ,
, ,则
,则 ;④若
;④若 ,
, ,则
,则 ;⑤若
;⑤若 与
与 异面,则至多有一条直线与
异面,则至多有一条直线与 、
、 都垂直.其中真命题是 .(把符合条件的序号都填上)
都垂直.其中真命题是 .(把符合条件的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com