
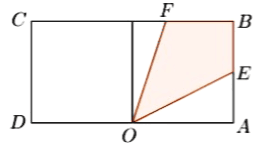
【题目】如图,三棱柱ABC﹣A1B1C1的侧面AA1B1B是菱形,侧面AA1C1C是矩形,平面AA1C1C⊥平面AA1B1B,∠BAA1![]() ,AA1=2AC=2,O为AA1的中点.
,AA1=2AC=2,O为AA1的中点.
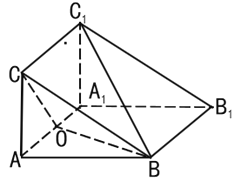
(1)求证:OC⊥BC1;
(2)求点C1到平面ABC的距离.
【答案】(1)证明见解析 (2)![]()
![]()
【解析】
(1)连接![]() ,AA1=2AC=2,O为AA1的中点,可得
,AA1=2AC=2,O为AA1的中点,可得![]() ,可证
,可证![]() ,侧面AA1B1B是菱形,
,侧面AA1B1B是菱形,![]() ,有
,有![]() ,结合平面AA1C1C⊥平面AA1B1B,可证
,结合平面AA1C1C⊥平面AA1B1B,可证
![]() 平面AA1C1C,可得
平面AA1C1C,可得![]() ,进而有
,进而有![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)![]() ,可证
,可证![]() 平面
平面![]() ,点C1到平面ABC的距离与点A1到平面ABC的距离相等,由(1)
,点C1到平面ABC的距离与点A1到平面ABC的距离相等,由(1)![]() 平面AA1C1C,求出
平面AA1C1C,求出![]() 的面积,用等体积法
的面积,用等体积法
![]() ,即可求解.
,即可求解.
(1)证明:连接![]() ,AA1=2AC=2,O为AA1的中点,
,AA1=2AC=2,O为AA1的中点,
![]() ,
,![]() ,
,
因为侧面AA1B1B是菱形,![]() ,
,
所以![]() 为等边三角形,O为AA1的中点,
为等边三角形,O为AA1的中点,
所以![]() ,平面AA1C1C⊥平面AA1B1B,
,平面AA1C1C⊥平面AA1B1B,
平面AA1C1C![]() 平面AA1B1B
平面AA1B1B![]() 平面AA1B1B,
平面AA1B1B,
所以![]() 平面AA1C1C,同理可证
平面AA1C1C,同理可证![]() 平面AA1B1B,
平面AA1B1B,
![]() 平面AA1C1C,所以
平面AA1C1C,所以![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]()
![]() ;
;
(2)因为侧面AA1C1C是矩形,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
点C1到平面ABC的距离与点A1到平面ABC的距离相等,
设C1到平面ABC的距离为![]() ,
,
由(1)得![]() 平面AA1C1C,
平面AA1C1C,![]() 平面AA1B1B,
平面AA1B1B,
所以![]() ,
,![]()
![]() ,
,
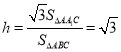 ,
,
所以点C1到平面ABC的距离为![]() .
.


科目:高中数学 来源: 题型:
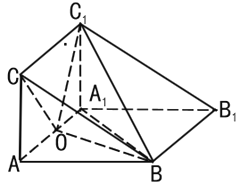
【题目】某专卖店销售一新款服装,日销售量(单位为件)f(n) 与时间n(1≤n≤30、n![]() N*)的函数关系如下图所示,其中函数f(n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
N*)的函数关系如下图所示,其中函数f(n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f(n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:存在实数
的全体:存在实数![]() 、
、![]() ,对于定义域内任意
,对于定义域内任意![]() ,均有
,均有![]() 成立,称数对
成立,称数对![]() 为函数
为函数![]() 的“伴随数对”.
的“伴随数对”.
(1)判断函数![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)若函数![]() ,求满足条件的函数
,求满足条件的函数![]() 的所有“伴随数对”;
的所有“伴随数对”;
(3)若![]() 、
、![]() 都是函数
都是函数![]() 的“伴随数对”,当
的“伴随数对”,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,求当
,求当![]() 时,函数
时,函数![]() 的解析式和零点.
的解析式和零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为实数,函数
为实数,函数![]() ,且函数
,且函数![]() 是偶函数,函数
是偶函数,函数![]() 在区间
在区间![]() 上是减函数,且在区间
上是减函数,且在区间![]() 上是增函数.
上是增函数.
(1)求函数![]() 的解析式;
的解析式;
(2)求实数![]() 的值;
的值;
(3)设![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在区间
在区间![]() 上有最小值-2?若存在,求出
上有最小值-2?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(3)若探照灯每9分钟旋转“一个来回”(![]() 自
自![]() 转到
转到![]() ,再回到
,再回到![]() ,称“一个来回”,忽略
,称“一个来回”,忽略![]() 在
在![]() 及
及![]() 处所用的时间),且转动的角速度大小一定,设
处所用的时间),且转动的角速度大小一定,设![]() 边上有一点
边上有一点![]() ,且
,且![]() ,求点
,求点![]() 在“一个来回”中被照到的时间.
在“一个来回”中被照到的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 函数
函数![]() ,函数
,函数![]() 的值域为
的值域为![]() ,
,
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 的解集
的解集![]() ,求实数
,求实数![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为
)的焦距为![]() ,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于
,且右焦点F与短轴的两个端点组成一个正三角形.若直线l与椭圆C交于![]() 、
、![]() ,且在椭圆C上存在点M,使得:
,且在椭圆C上存在点M,使得:![]() (其中O为坐标原点),则称直线l具有性质H.
(其中O为坐标原点),则称直线l具有性质H.
(1)求椭圆C的方程;
(2)若直线l垂直于x轴,且具有性质H,求直线l的方程;
(3)求证:在椭圆C上不存在三个不同的点P、Q、R,使得直线![]() 、
、![]() 、
、![]() 都具有性质H.
都具有性质H.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(1)设![]() ,判断
,判断![]() 在
在![]() 上是否为有界函数,若是,请说明理由,并写出
上是否为有界函数,若是,请说明理由,并写出![]() 的所有上界
的所有上界![]() 的集合;若不是,也请说明理由;
的集合;若不是,也请说明理由;
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com