
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形ABC所在的平面互相垂直,
所在的平面与正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
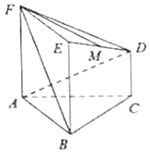
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:证明线面平则只需在平面内找一线与之平行即可,通常找中位线和建立平行四边形来证明,本题中可以容易发现连接AE交BF于点N,连接MN,可证MN为中位线;(2)二面角的问题通常借助于空间坐标系来求解,本题中可建立如图的坐标系,然后求出各面的法向量,再根据向量的夹角公式即可得出结论
解析:(1)连接AE交BF于点N,连接MN.
因为ABEF是正方形,所以N是AE的中点,
又M是ED的中点,所以MN∥AD.
因为AD平面BFM,MN![]() 平面BFM,
平面BFM,
所以AD∥平面BFM.
(2)因为ABEF是正方形,所以BE⊥AB,
因为平面ABEF⊥平面ABC,平面ABEF∩平面ABC=AB,
所以BE⊥平面ABC,因为CD∥BE,所以取BC的中点O,
连接OM,则OM⊥平面ABC,因为△ABC是正三角形,所以OA⊥BC,
所以以O为坐标原点建立如图所示的空间直角坐标系:
设CD=1,则B(0,1,0),E(0,1,2),D(0,﹣1,1),
![]() ,
,![]() .
.
设平面BMF的一个法向量为![]() ,
,
则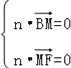 ,所以
,所以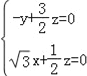 ,
,
令![]() ,则z=﹣6,y=﹣9,所以
,则z=﹣6,y=﹣9,所以![]() .
.
又因为![]() 是平面BME的法向量,
是平面BME的法向量,
所以![]() .
.
所以二面角E﹣BM﹣F的余弦值为![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+10x+10y+34=0.
(Ⅰ)试写出圆C的圆心坐标和半径;
(Ⅱ)圆D的圆心在直线x=-5上,且与圆C相外切,被x轴截得的弦长为10,求圆D的方程;
(Ⅲ)过点P(0,2)的直线交(Ⅱ)中圆D于E,F两点,求弦EF的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若对于任意的
,若对于任意的![]() ,,当
,,当![]() 时,都有
时,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上为非减函数.设函数
上为非减函数.设函数![]() 在
在![]() 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,则
,则![]() 等于( ).
等于( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
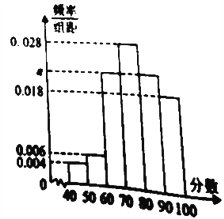
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
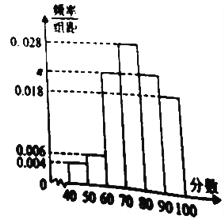
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程是 ![]() (φ为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标系方程是
(φ为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标系方程是 ![]() ,正方形ABCD的顶点都在C1上,且A,B,C,D依逆时针次序排列,点A的极坐标为
,正方形ABCD的顶点都在C1上,且A,B,C,D依逆时针次序排列,点A的极坐标为 ![]() .
.
(1)求点A,B,C,D的直角坐标;
(2)设P为C2上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式an=5﹣n,其前n项和为Sn , 将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn , 若存在m∈N* , 使对任意n∈N* , 总有Sn<Tn+λ恒成立,则实数λ的取值范围是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com