
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知2ccosA+a=2b
(1)求角C的值;
(2)若c=2,且△ABC的面积为 ![]() ,求a,b.
,求a,b.
【答案】
(1)解:∵2ccosA+a=2b,
∴2sinCcosA+sinA=2sinB,
∴2sinCcosA+sinA=2sin(A+C),
即2sinCcosA+sinA=2sinAcosC+2cosAsinC,
∴sinA=2sinAcosC,
∴ ![]() ,
,
又∵C是三角形的内角,
∴ ![]()
(2)解:∵ ![]() ,∴
,∴ ![]() ,∴ab=4,
,∴ab=4,
又∵c2=a2+b2﹣2abcosC,
∴4=(a+b)2﹣2ab﹣ab,
∴a+b=4,
∴a=b=2.
【解析】(1)利用两角和的正弦函数公式,正弦定理,三角形内角和定理化简已知等式可得sinA=2sinAcosC,由于sinA≠0,解得 ![]() ,又C是三角形的内角,即可得解C的值.(2)利用三角形面积公式可求ab=4,又由余弦定理可解得a+b=4,联立即可解得a,b的值.
,又C是三角形的内角,即可得解C的值.(2)利用三角形面积公式可求ab=4,又由余弦定理可解得a+b=4,联立即可解得a,b的值.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】有一解三角形的题目因纸张破损,有一条件不清,具体如下:在△ABC中,已知a= ![]() ,2cos2
,2cos2 ![]() =(
=( ![]() ﹣1)cosB,c= , 求角A,若该题的答案是A=60°,请将条件补充完整.
﹣1)cosB,c= , 求角A,若该题的答案是A=60°,请将条件补充完整.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1,2,3,4,5的卡片,这5张卡片除号码外完全相同,现进行有放回的连续抽取两次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求条件“取出卡片的号码之和不小于7或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从吉安市某校高一的1000名学生随机抽取50名分析期中考试数学成绩,被抽取学生成绩全部介于95分和135分之间,将抽取的成绩分成八组:第一组[95,100],第二组[100,105],…,第八组[130,135],如图是按上述分组得到的频率分布直方图的一部分,已知前三组的人数成等差数列,第六组的人数为4人,第一组的人数是第七组、第八组人数之和. 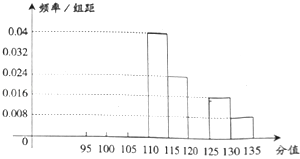
(1)在图上补全频率分布直方图,并估计该校1000名学生中成绩在120分以上(含120分)的人数;
(2)若从成绩属于第六组,第八组的所有学生中随机抽取两名学生,记他们的成绩分别为x,y,事件G=||x﹣y|≤5|,求P(G).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是双曲线 ![]() 的左右焦点,A为双曲线的右顶点,线段AF2的垂直平分线交双曲线与P,且|PF1|=3|PF2|,则该双曲线的离心率是( )
的左右焦点,A为双曲线的右顶点,线段AF2的垂直平分线交双曲线与P,且|PF1|=3|PF2|,则该双曲线的离心率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】富华中学的一个文学兴趣小组中,三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究,并且他们选择的名家各不相同.三位同学一起来找图书管理员刘老师,让刘老师猜猜他们三人各自的研究对象.刘老师猜了三句话:“①张博源研究的是莎士比亚;②刘雨恒研究的肯定不是曹雪芹;③高家铭自然不会研究莎士比亚.”很可惜,刘老师的这种猜法,只猜对了一句.据此可以推知张博源、高家铭和刘雨恒分别研究的是__________.(A莎士比亚、B雨果、C曹雪芹,按顺序填写字母即可.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导函数f′(x)是二次函数,如图是f′(x)的大致图象,若f(x)的极大值与极小值的和等于 ![]() ,则f(0)的值为( )
,则f(0)的值为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验杯足球赛采用七人制淘汰赛规则,某场比赛中一班与二班在常规时间内战平,直接进入点球决胜环节,在点球决胜环节中,双方首先轮流罚点球三轮,罚中更多点球的球队获胜;若双方在三轮罚球中未分胜负,则需要进行一对一的点球决胜,即双方各派处一名队员罚点球,直至分出胜负;在前三轮罚球中,若某一时刻胜负已分,尚未出场的队员无需出场罚球(例如一班在先罚球的情况下,一班前两轮均命中,二班前两轮未能命中,则一班、二班的第三位同学无需出场).由于一班同学平时踢球热情较高,每位队员罚点球的命中率都能达到0.8,而二班队员的点球命中串只有0.5,比赛时通过抽签决定一班在每一轮都先罚球.
(1)定义事件![]() 为“一班第三位同学没能出场罚球”,求事件
为“一班第三位同学没能出场罚球”,求事件![]() 发生的概率;
发生的概率;
(2)若两队在前三轮点球结束后打平,则进入一对一点球决胜,一对一球决胜由没有在之前点球大战中出场过的队员主罚点球,若在一对一点球决胜的某一轮中,某对队员射入点球且另一队员未能射入,则比赛结束;若两名队员均射入或者均射失点球,则进行下一轮比赛. 若直至双方场上每名队员都已经出场罚球,则比赛亦结束,双方通过抽签决定胜负,本场比赛中若已知双方在点球大战,以随机变量![]() 记录双方进行一对一点球决胜的轮数,求
记录双方进行一对一点球决胜的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com