
【题目】某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
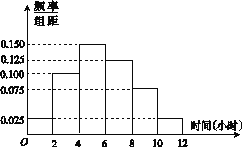
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4小时的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
【答案】(1)90;(2)0.75;(3)![]() %.
%.
【解析】
试题分析:(1)由题知,抽样比例为50:1,分层抽样是按照男女生比例来比例来抽样的,所以所抽300名学生中,男生与女生比例为10500:4500,可求出女生人数为![]() ;(2)观察频率分布直方图,找出每周平均体育运动不超过4小时的所有小矩形高即为频率/组距,这些小矩形的面积和即为每周平均体育运动不超过4小时的频率,1减去这个频率就是一周体育运动时间超过4小时的频率;(3)根据频率分之直方图计算出这300名学生中每周平均体育运动时间超过4小时以及不超过4小时的人数,列出
;(2)观察频率分布直方图,找出每周平均体育运动不超过4小时的所有小矩形高即为频率/组距,这些小矩形的面积和即为每周平均体育运动不超过4小时的频率,1减去这个频率就是一周体育运动时间超过4小时的频率;(3)根据频率分之直方图计算出这300名学生中每周平均体育运动时间超过4小时以及不超过4小时的人数,列出![]() 表格,并代入公式
表格,并代入公式 中,得到样本观测值,将该值与表中概率为0.95的值比较,可得出有
中,得到样本观测值,将该值与表中概率为0.95的值比较,可得出有![]() %的把握认为“该校学生的每周平均体育运动时间与性别有关”.
%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
试题解析:(1)![]() ,所以应收集
,所以应收集![]() 位女生的样本数据.
位女生的样本数据.
(2)由频率分布直方图得![]() ,所以该校学生每周平均体育运动时间超过
,所以该校学生每周平均体育运动时间超过![]() 小时的概率的估计值为
小时的概率的估计值为![]() .
.
(3)由(2)知,![]() 位学生中有
位学生中有![]() 人的每周平均体育运动时间超过
人的每周平均体育运动时间超过![]() 小时,
小时,![]() 人的每周平均体育运动时间不超过
人的每周平均体育运动时间不超过![]() 小时.又因为样本数据中有
小时.又因为样本数据中有![]() 份是关于男生的,
份是关于男生的,![]() 份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
份是关于女生的,所以每周平均体育运动时间与性别列联表如下:

结合列联表可算得![]()
所以有![]() %的把握认为“该校学生的每周平均体育运动时间与性别有关”.
%的把握认为“该校学生的每周平均体育运动时间与性别有关”.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知曲线C1:y=![]() (x>0)及曲线C2:y=
(x>0)及曲线C2:y=![]() (x>0).C1上的点Pn的横坐标为an,
(x>0).C1上的点Pn的横坐标为an,![]() 过C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再过点Qn作直线平行于y轴,交曲线C1于点Pn+1.
过C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再过点Qn作直线平行于y轴,交曲线C1于点Pn+1.
试求an+1与an之间的关系,并证明a2n-1<![]() <a2n(n∈N+).
<a2n(n∈N+).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年,首都北京经历了59年来雾霾天气最多的一个月.经气象局统计,北京市从1月1日至1月30日的30天里有26天出现雾霾天气,《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级,其中,中度污染(四级)指数为151~200;重度污染(五级)指数为201~300;严重污染(六级)指数大于300.下面表1是某观测点记录的4天里AQI指数M与当天的空气水平可见度y(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数的统计结果.
表1
AQI指数M | 900 | 700 | 300 | 100 |
空气可见度y/千米 | 0.5 | 3.5 | 6.5 | 9.5 |
表2
AQI指数 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设变量x=![]() ,根据表1的数据,求出y关于x的线性回归方程;
,根据表1的数据,求出y关于x的线性回归方程;
(2)根据表2估计这30天AQI指数的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知恒等式(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n .
(1)求a1+a2+a3+…+a2n和a2+2a3+22a4+…+22n﹣2a2n的值;
(2)当n≥6时,求证: ![]() a2+2A
a2+2A ![]() a3+…+22n﹣2
a3+…+22n﹣2 ![]() a2n<49n﹣2 .
a2n<49n﹣2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不为0的数列{an}满足a1=a,a2=b,且an2=an﹣1an+1+λ(n≥2,n∈N),其中λ∈R.
(1)若λ=0,求证:数列{an}是等比数列;
(2)求证:数列{an}是等差数列的充要条件是λ=(b﹣a)2;
(3)若数列{bn}为各项均为正数的等比数列,且对任意的n∈N* , 满足bn﹣an=1,求证:数列{(﹣1)nanbn}的前2n项和为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c(a<b<c).已知向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA)满足
=(cosC,cosA)满足 ![]()
![]() =
= ![]() (a+c).
(a+c).
(1)求证:a+c=2b;
(2)若2csinA﹣ ![]() a=0,且c﹣a=8,求△ABC的面积S.
a=0,且c﹣a=8,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Q2=![]() 称为x,y的二维平方平均数,A2=
称为x,y的二维平方平均数,A2=![]() 称为x,y的二维算术平均数,G2=
称为x,y的二维算术平均数,G2=![]() 称为x,y的二维几何平均数,H2=
称为x,y的二维几何平均数,H2=![]() 称为x,y的二维调和平均数,其中x,y均为正数.
称为x,y的二维调和平均数,其中x,y均为正数.
(1)试判断G2与H2的大小,并证明你的猜想.
(2)令M=A2﹣G2,N=G2﹣H2,试判断M与N的大小,并证明你的猜想.
(3)令M=A2﹣G2,N=G2﹣H2,P=Q2﹣A2,试判断M、N、P三者之间的大小关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com