
【题目】已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出f(x)的周期、振幅、初相、对称轴;
(3)此函数图象由y=sinx的图象怎样变换得到?(注:y轴上每一竖格长为1)

【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析.
【解析】试题分析:
(1)由题意结合五点法列表,据此绘制函数图象即可;
(2)结合函数的解析式可得函数的周期为![]() ,振幅为3,初相为
,振幅为3,初相为![]() ,对称轴方程为:
,对称轴方程为:![]() .
.
(3)结合三角函数的变换性质可知变换过程如下:由y=sinx在[0,2π]上的图象向左平移![]() 个单位,把横坐标伸长为原来的2倍,把纵坐标伸长为原来的3倍,向上平移3个单位,即可得到
个单位,把横坐标伸长为原来的2倍,把纵坐标伸长为原来的3倍,向上平移3个单位,即可得到![]() 的图象.
的图象.
试题解析:
(1)令![]() 取0,
取0,![]() ,π,
,π,![]() ,2π,列表如下:
,2π,列表如下:
| 0 |
| π |
| 2π |
x |
|
|
|
|
|
| 3 | 6 | 3 | 0 | 3 |
在一个周期内的闭区间上的图象如下图所示:
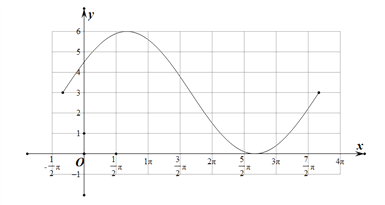
(2)∵函数![]() 中,A=3,B=3,ω=
中,A=3,B=3,ω=![]() ,φ=
,φ=![]() .
.
∴函数f(x)的周期T=4π,振幅为3,初相为![]() ,
,
对称轴满足:![]() ,
,
据此可得对称轴方程为:![]() .
.
(3)此函数图象可由y=sinx在[0,2π]上的图象经过如下变换得到:
①向左平移![]() 个单位,得到y=sin(x+
个单位,得到y=sin(x+![]() )的图象;
)的图象;
②再保持纵坐标不变,把横坐标伸长为原来的2倍得到y=![]() 的图象;
的图象;
③再保持横坐标不变,把纵坐标伸长为原来的3倍得到y=![]() 的图象;
的图象;
④再向上平移3个单位,得到![]() 的图象.
的图象.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:在定义域
满足:在定义域![]() 内存在实数
内存在实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“
为“![]() 的饱和函数”.给出下列四个函数:①
的饱和函数”.给出下列四个函数:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() .其中是“
.其中是“![]() 的饱和函数”的所有函数的序号是______________.
的饱和函数”的所有函数的序号是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为 ![]() 的等比数列{an}不是递减数列,其前n项和为Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)若实数a使得a>Sn+ ![]() 对任意n∈N*恒成立,求a的取值范围.
对任意n∈N*恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 ![]() 以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
(1)写出直线l的极坐标方程与曲线C的普通方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其导函数f′(x)的部分图象如图所示,则函数f(x)的解析式为( ) 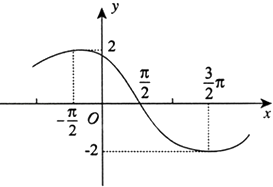
A.f(x)=4sin( ![]() x+
x+ ![]() π)
π)
B.f(x)=4sin( ![]() x+
x+ ![]() )
)
C.f(x)=4sin( ![]() x+
x+ ![]() )
)
D.f(x)=4sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=x﹣ln x﹣2.
(Ⅰ)求函数 f ( x) 的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在区间(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F为双曲线 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )
=1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )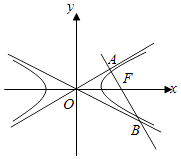
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.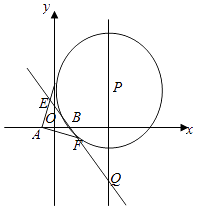
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,有2Sn=n2+n+4(n∈+)
(1)求数列的通项公式an;
(2)若bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com