Question

【题目】已知函数,当x = -1时取得极大值7，当x = 3时取得极小值；

（1）求a,b的值；

（2）求f(x)的极小值。

Answer 1

【答案】（1）；（2）.

【解析】

利用函数f（x）在x=x0取得极值的充要条件f′（x0）=0且f′（x）在x=x0的左右附近符号相反即可得出a，b的值，再利用极大值即可得到c，从而得出答案．

(1)∵f(x) = x3+ ax2+bx + c ,∴f′ (x) = 3x2+2ax +b

∵当x =- 1 时函数取得极大值7，当x = 3时取得极小值

∴x =- 1 和x = 3是方程f′ (x)=0的两根，有

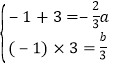∴， ∴f(x) = x3-3x2-9x+c.

(2)∵当x = -1时，函数取极大值7，∴(-1)3–3(-1)2–9(-1)+c= 7,∴c=2.

此时函数f(x)的极小值为：f（3）= 33-3×32-9×3×2=-25.