练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
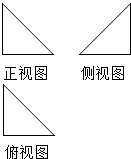
    18．一个空间几何体的三视图如图所示，其正视图、侧视  图、俯视图均为等腰直角三角形，且直角边长都为1，则它的外接球的表面积是（　　）
    A．3πB．πC．2πD．4π

    分析 由正视图、侧视图、俯视图均为等腰直角三角形，且直角边长都为1，我们可以把它看成一个棱长为1的正方体的一角，故其外接球即为棱长为1的正方体的外接球．

    解答 解：由正视图、侧视图、俯视图均为直角边长为1等腰直角三角形，
    故其外接球即为棱长为1的正方体的外接球，
    则2R=$\sqrt{3}$，
    ∴外接球的表面积S=4πR2=3π，
    故选：A

    点评 本题考查的知识点是由三视图求面积，其中利用补足法，将该几何体的外接球，转化为棱长为1的正方体的外接球，是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．对于任意实数a、b，（a-b）2≥kab均成立，则实数k的取值范围是（　　）
    A．{-4，0}B．[-4，0]C．（-∞，0]D．（-∞，-4]∪[0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在平面直角坐标系xOy中，对于点P（x0，y0）、直线l：ax+by+c=0，我们称$δ=\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$为点P（x0，y0）到直线l：ax+by+c=0的方向距离．
    （1）设椭圆$\frac{x^2}{4}+{y^2}=1$上的任意一点P（x，y）到直线l1：x-2y=0，l2：x+2y=0的方向距离分别为δ1、δ2，求δ1δ2的取值范围．
    （2）设点E（-t，0）、F（t，0）到直线l：xcosα+2ysinα-2=0的方向距离分别为η1、η2，试问是否存在实数t，对任意的α都有η1η2=1成立？若存在，求出t的值；不存在，说明理由．
    （3）已知直线l：mx-y+n=0和椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），设椭圆E的两个焦点F1，F2到直线l的方向距离分别为λ1、λ2满足${λ_1}{λ_2}＞{b^2}$，且直线l与x轴的交点为A、与y轴的交点为B，试比较|AB|的长与a+b的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

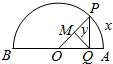    6．如图，AB为定圆O的直径，点P为半圆AB上的动点．过点P作AB的垂线，垂足为Q，过Q作OP的垂线，垂足为M．记弧AP的长为x，线段QM的长为y，则函数y=f（x）的大致图象是（　　）
    A．B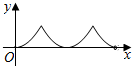．C．D．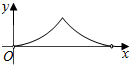

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．抛物线x2=4y上与焦点的距离等于4的点的纵坐标是（　　）
    A．lB．KC．3D．y-1=k（x-2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下列函数中，在其定义域内既是奇函数又是增函数的是（　　）
    A．y=x+x3B．y=3xC．y=log2xD．$y=-\frac{1}{x}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．空间中，如果两个角的两条边分别对应平行，那么这两个角（　　）
    A．相等B．互补C．相等或互补D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．将长AB=4π，宽BC=π的矩形ABCD，卷成圆柱的侧面，则所得圆柱的体积最大值为4π2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

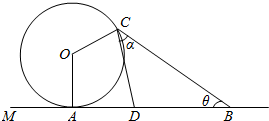    8．如图，在一条景观道的一端有一个半径为50米的圆形摩天轮O，逆时针15分钟转一圈，从A处进入摩天轮的座舱，OA垂直于地面AM，在距离A处150米处设置了一个望远镜B．
    （1）同学甲打算独自乘坐摩天轮，但是其母亲不放心，于是约定在登上摩天轮座舱5分钟后，在座舱内向其母亲挥手致意，而其母亲则在望远镜B中仔细观看．问望远镜B的仰角θ应调整为多少度？（精确到1度）
    （2）在同学甲向其母亲挥手致意的同时，同一座舱的另一名乘客乙在拍摄地面上的一条绿化带BD，发现取景的视角α恰为45°，求绿化带BD的长度（精确到1米）．

    查看答案和解析>>

    同步练习册答案