
【题目】若函数f(x)= ![]() 恰有2个零点,则实数a的取值范围是 .
恰有2个零点,则实数a的取值范围是 .
【答案】[ ![]() ,1)∪[3,+∞)
,1)∪[3,+∞)
【解析】解:①当a≤0时,f(x)>0恒成立,
故函数f(x)没有零点;②当a>0时,3x﹣a=0,
解得,x=log3a,又∵x<1;
∴当a∈(0,3)时,log3a<1,
故3x﹣a=0有解x=log3a;
当a∈[3,+∞)时,log3a≥1,
故3x﹣a=0在(﹣∞,1)上无解;
∵x2﹣3ax+2a2=(x﹣a)(x﹣2a),
∴当a∈(0, ![]() )时,
)时,
方程x2﹣3ax+2a2=0在[1,+∞)上无解;
当a∈[ ![]() ,1)时,
,1)时,
方程x2﹣3ax+2a2=0在[1,+∞)上有且仅有一个解;
当a∈[1,+∞)时,
方程x2﹣3ax+2a2=0在[1,+∞)上有且仅有两个解;
综上所述,
当a∈[ ![]() ,1)或a∈[3,+∞)时,
,1)或a∈[3,+∞)时,
函数f(x)= ![]() 恰有2个零点,
恰有2个零点,
所以答案是:[ ![]() ,1)∪[3,+∞).
,1)∪[3,+∞).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示:
根据下表信息解答以下问题:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
(1)从该单位任选两名职工,用η表示这两人休年假次数之和,记“函数f(x)=x2﹣ηx﹣1在区间(4,6)上有且只有一个零点”为事件A,求事件A发生的概率P;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,满足2asinA=(2b﹣ ![]() c)sinB+(2c﹣
c)sinB+(2c﹣ ![]() b)sinC. (Ⅰ)求角A的大小;
b)sinC. (Ⅰ)求角A的大小;
(Ⅱ)若a=2,b=2 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是( )
A.(﹣∞,﹣3)∪(0,3)
B.(﹣∞,﹣3)∪(3,+∞)
C.(﹣3,0)∪(3,+∞)
D.(﹣3,0)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 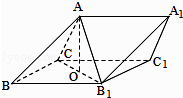
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0,
(1)求l2的方程,使得:①l2与l1平行,且过点(﹣1,3); ②l2与l1垂直,且l2与两坐标轴围成的三角形面积为4;
(2)直线l1与两坐标轴分别交于A、B 两点,求三角形OAB(O为坐标原点)内切圆及外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2 , x1+x2=1﹣a,则( )
A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.f(x1)<f(x2)和f(x1)=f(x2)都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com