
科目:高中数学 来源:不详 题型:解答题
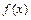 ,若存在闭区间
,若存在闭区间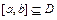 和常数
和常数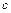 ,使得对任意
,使得对任意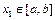 ,都有
,都有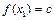 ,
,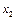 ∈D,当
∈D,当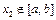 时,
时,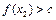 恒成立,则称函数
恒成立,则称函数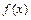 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.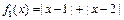 和
和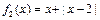 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 基本费
基本费 超额费
超额费 定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量
定额损耗费,且有如下三条规定:① 若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;② 若每月用水量超过
元;② 若每月用水量超过 立方米时,除了付基本费和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费和定额损耗费外,超过部分每立方米付 元的超额费;③ 每户每月的定额损耗费
元的超额费;③ 每户每月的定额损耗费 不超过5元.
不超过5元. (元)与月用水量
(元)与月用水量 (立方米)的函数关系;
(立方米)的函数关系; 的费用如下表所示:
的费用如下表所示:| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| 三 | 2.5 | 11 |
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,f2(x)=
,f2(x)= (其中m ∈R且m≠0).
(其中m ∈R且m≠0). 当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.
当m≥2时,若对于任意的x1∈[2,+∞),总存在唯一的x2∈(-∞,2),使得g(x1)=g(x2)成立.试求m的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
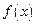 满足
满足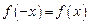 ,且在[1,2]上单调递增,则
,且在[1,2]上单调递增,则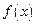 在[-2,-1]上的最小值是( )
在[-2,-1]上的最小值是( )| A.- f (1) | B. f (1) | C.-f (2) | D. f (2) f (2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的反函数
的反函数  ( )
( ) 是奇函数,它在(0, +∞)上是增函数 D 是偶函数,它在(0, +∞)上是增函数
是奇函数,它在(0, +∞)上是增函数 D 是偶函数,它在(0, +∞)上是增函数查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com