Question

（04年全国卷III理）（12分）

三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3.

(1)求证 AB⊥BC ；

(II)如果 AB=BC=2，求AC与侧面PBC所成角的大小．

Answer 1

解析：⑴证明：取AC中点O, 连结PO、BO.

∵PA＝PC　∴PO⊥AC　

又∵侧面PAC⊥底面ABC

∴PO⊥底面ABC

又PA＝PB＝PC　∴AO＝BO＝CO

∴△ABC为直角三角形　∴AB⊥BC

　

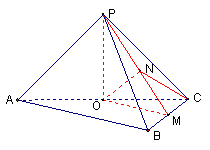
⑵解：取BC的中点为M，连结OM,PM，所以有OM=AB=，AO=

∴

由⑴有PO⊥平面ABC,OM⊥BC，由三垂线定理得PM⊥BC

∴平面POM⊥平面PBC，又∵PO=OM=.

∴△POM是等腰直角三角形，取PM的中点N，连结ON, NC

则ON⊥PM, 又∵平面POM⊥平面PBC, 且交线是PM, ∴ON⊥平面PBC

∴∠ONC即为AC与平面PBC所成的角.

∴  ∴.

故AC与平面PBC所成的角为.