
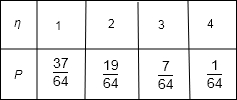
| ||||||
| 43 |
| 19 |
| 64 |
| ||||||
| 43 |
| 37 |
| 64 |
| ||||||
| 43 |
| 7 |
| 64 |
| ||
| 43 |
| 1 |
| 64 |
| 25 |
| 16 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)一个袋中有8个大小相同的小球,其中红球1个,白球和黑球若干,现从袋中有放回地取球,每次随机取一个,又知连续取两次都是白球的概率为![]() :
:
(1)求该口袋内白球和黑球的个数;
(2)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率;
(3)现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得黑球时游戏终止,每个球在每一次被取出的机会均相同.求当游戏终止时,取球次数不多于3的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
一个不透明的口袋中有若干个红球和黑 球,从中摸出一个,每个球被摸出的可能性是相同的.现从中摸出两个球,均是红球的概率为![]() ,已知袋中红球有3个,则袋中共有球的个数为
,已知袋中红球有3个,则袋中共有球的个数为
A. 4 B. 5 C. 6 D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
(14分)一个袋中有8个大小相同的小球,其中红球1个,白球和黑球若干,现从袋中有放回地取球,每次随机取一个,又知连续取两次都是白球的概率为1/4.
(Ⅰ)求该口袋内白球和黑球的个数;
(Ⅱ)规定取出1个红球得2分,取出1个白色球得1分,取出1个黑色球得0分,连续取三次分数之和为4分的概率;
(Ⅲ)现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取,乙后取,然后甲在取,直到两个小朋友中有1人取得黑球时游戏终止,每个球在每一次被取出的机会均相同,求当游戏终止时,取球次数不多于3次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com