
【题目】已知曲线C1的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
【答案】解:(Ⅰ)曲线C1的参数方程为 ![]() (t为参数), 则曲线C1的普通方程为(x﹣5)2+(y﹣4)2=25,
(t为参数), 则曲线C1的普通方程为(x﹣5)2+(y﹣4)2=25,
曲线C1的极坐标方程为ρ2﹣10ρcosθ﹣8ρsinθ+16=0.
(Ⅱ)曲线C1的极坐标方程ρ2﹣10ρcosθ﹣8ρsinθ+16=0,曲线C2的极坐标方程为ρ=2cosθ,联立得 ![]() ,又θ∈[0,2π),则θ=0或
,又θ∈[0,2π),则θ=0或 ![]() ,
,
当θ=0时,ρ=2;当 ![]() 时,
时, ![]() ,所以交点坐标为(2,0),
,所以交点坐标为(2,0), ![]()
【解析】. (Ⅰ)把C1的参数方程化为普通方程,再化为极坐标方程;(Ⅱ)曲线C1的极坐标方程ρ2﹣10ρcosθ﹣8ρsinθ+16=0,曲线C2的极坐标方程为ρ=2cosθ,联立,即可求C1与C2交点的极坐标.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,已知点P(0, ![]() ),曲线C的参数方程为
),曲线C的参数方程为 ![]() (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ= ![]() .
.
(Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照[0,100),[100,200),[200,300),[300,400),[400,500),[500,600),[600,700),[700,800),[800,900]分成9组,制成了如图所示的频率分布直方图. 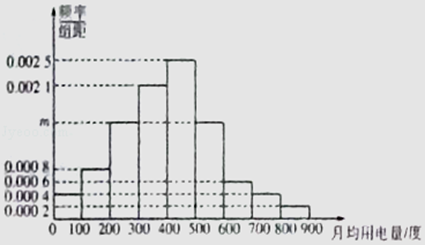
(Ⅰ)求直方图中m的值并估计居民月均用电量的中位数;
(Ⅱ)从样本里月均用电量不低于700度的用户中随机抽取4户,用X表示月均用电量不低于800度的用户数,求随机变量X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)的导函数为f'(x),满足x2f'(x)+xf(x)=lnx,f(e)= ![]() ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 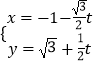 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 ![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设点为P(x,y)为直线l与圆C所截得的弦上的动点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},a1=﹣ll,公差d≠0,且a2 , a5 , a6成等比数列.
(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是( ) ①x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
A.①③
B.①④
C.②④
D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com