
【题目】已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(﹣12,﹣15),则E的方程式为( )
A.![]()
B.![]()
C.![]()
D.![]()
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(1﹣ ![]() )+1,则f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
)+1,则f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
A.0
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)右顶点与右焦点的距离为
=1(a>b>0)右顶点与右焦点的距离为 ![]() ﹣1,短轴长为2
﹣1,短轴长为2 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为 ![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,三角形ABC为等腰直角三角形,AC=BC= ![]() ,AA1=1,点D是AB的中点.
,AA1=1,点D是AB的中点. 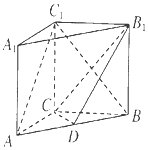
(1)求证:AC1∥平面CDB1;
(2)二面角B1﹣CD﹣B的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=2sin(180°﹣x)+cos(﹣x)﹣sin(450°﹣x)+cos(90°+x).
(1)若f(α)= ![]() α∈(0°,180°),求tanα;
α∈(0°,180°),求tanα;
(2)若f(α)=2sinα﹣cosα+ ![]() ,求sinαcosα的值.
,求sinαcosα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 、
、 ![]() 为平面向量,若存在不全为零的实数λ,μ使得λ
为平面向量,若存在不全为零的实数λ,μ使得λ ![]() +μ
+μ ![]() =0,则称
=0,则称 ![]() 、
、 ![]() 线性相关,下面的命题中,
线性相关,下面的命题中, ![]() 、
、 ![]() 、
、 ![]() 均为已知平面M上的向量. ①若
均为已知平面M上的向量. ①若 ![]() =2
=2 ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
②若 ![]() 、
、 ![]() 为非零向量,且
为非零向量,且 ![]() ⊥
⊥ ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
③若 ![]() 、
、 ![]() 线性相关,
线性相关, ![]() 、
、 ![]() 线性相关,则
线性相关,则 ![]() 、
、 ![]() 线性相关;
线性相关;
④向量 ![]() 、
、 ![]() 线性相关的充要条件是
线性相关的充要条件是 ![]() 、
、 ![]() 共线.
共线.
上述命题中正确的是(写出所有正确命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com