
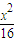 -
-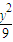 =1上求一点M,使它到左右两焦点的距离之比为3:2,并求M点到两准线的距离.
=1上求一点M,使它到左右两焦点的距离之比为3:2,并求M点到两准线的距离. ,a=4代入,求出点M的坐标后能得到双曲线准线方程,然后再求出点M(16,±3
,a=4代入,求出点M的坐标后能得到双曲线准线方程,然后再求出点M(16,±3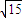 )到两条准线的距离.
)到两条准线的距离. ,a=4代入,得x1=16,y1=±3
,a=4代入,得x1=16,y1=±3 .
.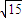 ).
).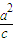 =±
=±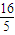 .
. )到准线的距离为12
)到准线的距离为12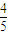 或19
或19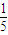 .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 8 |
| y2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 18 |
| y2 |
| 14 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省亳州市涡阳二中高二第二学期期末质量检测文科数学试题 题型:解答题
已知双曲线 与椭圆
与椭圆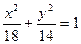 有共同的焦点,点
有共同的焦点,点 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)以P(1,2)为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
查看答案和解析>>
科目:高中数学 来源:2012届山东省高二下学期期末考试文科数学 题型:解答题
(本大题满分13分)
已知双曲线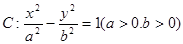 与椭圆
与椭圆 有共同的焦点,点
有共同的焦点,点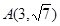 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)以P(1,2)为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com