
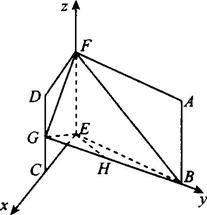
第18题图
(1)当平面BFG⊥平面BEG时,求G点的位置;
(2)在(1)的前提下,求直线GE与平面BFG所成的角.
答案:(1)建立如图所示的坐标系,有F(0,0,2)、E(0,0,0).
设G(1,0,z),则![]() =(1,0,z),
=(1,0,z),![]() =(0,2,0),
=(0,2,0),![]() =(0,-2,2).
=(0,-2,2).

第18题图
又设平面BEG的法向量为m=(a,b,c),则
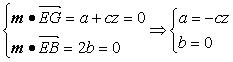 .
.
令c=1,得m=(-z,0,1).
设平面BFG的法向量为n=(p,q,r),则
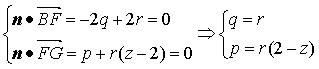 .
.
令r=1,得n=(2-z,1,1).
令m⊥n,得-z(2-z)+1=0![]() z=1.
z=1.
故当且仅当G为CD中点时,平面BFG⊥平面BEF.
(2)作EH⊥BG于H.
∴平面BFG⊥平面BEG,∴EH⊥平面BFG.
于是,∠EGH就是直线GE与平面BFG所成的角.
在ABGE中,∵EH·BG=BE·EG,
∴EH=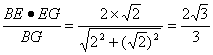
故sin∠EGH=![]() .
.
∴∠EGH=arcsin![]() .
.


科目:高中数学 来源: 题型:
 已知某几何体的直观图和三视图如图所示,其正视图为直角梯形,侧视图为等腰直角三角形,俯视图为矩形.
已知某几何体的直观图和三视图如图所示,其正视图为直角梯形,侧视图为等腰直角三角形,俯视图为矩形.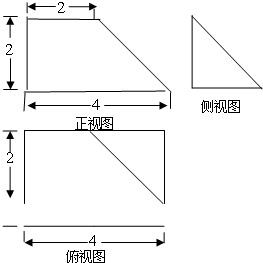
查看答案和解析>>
科目:高中数学 来源: 题型:044
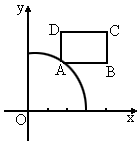
如图所示,设矩形
ABCD的顶点C坐标为(4,4),点A在圆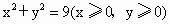 上移动,且AB、AD两边分别平行于x轴、y轴.求矩形ABCD面积的最小值及对应点A的坐标.
上移动,且AB、AD两边分别平行于x轴、y轴.求矩形ABCD面积的最小值及对应点A的坐标.
查看答案和解析>>
科目:高中数学 来源:浙江省杭州二中2011-2012学年高二上学期期中考试数学理科试题 题型:044
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示),将矩形折叠,使A点落在线段DC上.

(Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
(Ⅱ)设折痕线段为EF,记|EF|2=f(k),求f(k)的解析式.
查看答案和解析>>
科目:高中数学 来源:广东省汕头市金山中学2011-2012学年高二上学期12月月考数学理科试题 题型:044
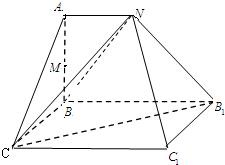
在平面上,将周长为24的矩形ABCD(AB>AD)沿对角线AC对折,使点B至B1处,AB1与DC交于点P(如图所示),设AD=x,DP=y.
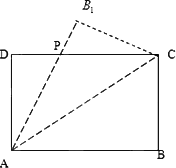
(1).将y表示成x的函数并写出x的取值范围.
(2).求△ADP面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com