
【题目】已知数列{xn}满足x1=1,x2=λ,并且 ![]() =λ
=λ ![]() (λ为非零常数,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比数列,求λ的值;
(λ为非零常数,n=2,3,4,…). (Ⅰ)若x1 , x3 , x5成等比数列,求λ的值;
(Ⅱ)设0<λ<1,常数k∈N* , 证明 ![]() .
.
【答案】解:(I)∵x1=1,x2=λ,并且 ![]() =λ
=λ ![]() (λ为非零常数,n=2,3,4,…). ∴x3=
(λ为非零常数,n=2,3,4,…). ∴x3= ![]() =λ3 , x4=
=λ3 , x4= 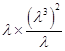 =λ6 , x5=
=λ6 , x5=  =λ10 .
=λ10 .
∵x1 , x3 , x5成等比数列,
∴ ![]() =x1x5 ,
=x1x5 ,
∴(λ3)2=1×λ10 , λ≠0,
化为λ4=1,
解得λ=±1.
(II)证明:设0<λ<1,常数k∈N* , ![]() =λ
=λ ![]() ,
, ![]() =λ.
=λ.
∴ ![]() =λλn﹣1=λn ,
=λλn﹣1=λn ,
∴xn= ![]() …
… ![]() x1=λn﹣1λn﹣2…λ1=
x1=λn﹣1λn﹣2…λ1= ![]() .
.
∴ ![]() =
= 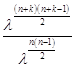 =
= ![]() .
.
∴ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]()
![]() <
< ![]()
![]() <
< ![]() .
.
【解析】(I)由于x1=1,x2=λ,并且 ![]() =λ
=λ ![]() (λ为非零常数,n=2,3,4,…).可得x3 , x4 , x5 . 由于x1 , x3 , x5成等比数列,可得
(λ为非零常数,n=2,3,4,…).可得x3 , x4 , x5 . 由于x1 , x3 , x5成等比数列,可得 ![]() =x1x5 , 代入解出即可得出.(II)设0<λ<1,常数k∈N* ,
=x1x5 , 代入解出即可得出.(II)设0<λ<1,常数k∈N* , ![]() =λ
=λ ![]() ,
, ![]() =λ.可得
=λ.可得 ![]() =λn , 利用“累乘求积”可得:xn=
=λn , 利用“累乘求积”可得:xn= ![]()
![]() …
… ![]() x1=
x1= ![]() .可得
.可得 ![]() =
= ![]() .再利用等比数列的前n项和公式即可得出.
.再利用等比数列的前n项和公式即可得出.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2(1)在直线l上任取两点A,B;(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是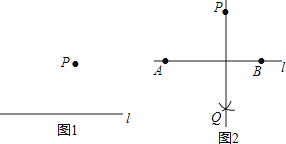
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且椭圆的长轴长为4.
的离心率互为倒数,且椭圆的长轴长为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() (
(![]() )为椭圆
)为椭圆![]() 上一点,求
上一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【江西省临川实验学校2017届高三第一次模拟考试数学(文)】已知抛物线![]() ,焦点为
,焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() 到
到![]() 的距离比
的距离比![]() 到直线
到直线![]() 的距离小1.
的距离小1.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 与
与![]() ,切点分别为
,切点分别为![]() ,求证:直线
,求证:直线![]() 恒过某一定点.
恒过某一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为![]() 且过点(4,-
且过点(4,- ![]() ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,
的图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
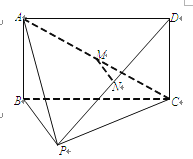
【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com