
ЁОЬтФПЁПЮЊСЫОЛЛЏПеЦјЃЌФГПЦбаЕЅЮЛИљОнЪЕбщЕУГіЃЌдквЛЖЈЗЖЮЇФкЃЌУПХчШї1ИіЕЅЮЛЕФОЛЛЏМСЃЌПеЦјжаЪЭЗХЕФХЈЖШy(ЕЅЮЛЃККСПЫ/СЂЗНУз)ЫцзХЪБМфx(ЕЅЮЛЃКЬь)БфЛЏЕФКЏЪ§ЙиЯЕЪННќЫЦЮЊyЃН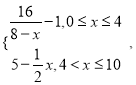 ШєЖрДЮХчШїЃЌдђФГвЛЪБПЬПеЦјжаЕФОЛЛЏМСХЈЖШЮЊУПДЮЭЖЗХЕФОЛЛЏМСдкЯргІЪБПЬЫљЪЭЗХЕФХЈЖШжЎКЭЃЎгЩЪЕбщжЊЃЌЕБПеЦјжаОЛЛЏМСЕФХЈЖШВЛЕЭгк4(КСПЫ/СЂЗНУз)ЪБЃЌЫќВХФмЦ№ЕНОЛЛЏПеЦјЕФзїгУЃЎ
ШєЖрДЮХчШїЃЌдђФГвЛЪБПЬПеЦјжаЕФОЛЛЏМСХЈЖШЮЊУПДЮЭЖЗХЕФОЛЛЏМСдкЯргІЪБПЬЫљЪЭЗХЕФХЈЖШжЎКЭЃЎгЩЪЕбщжЊЃЌЕБПеЦјжаОЛЛЏМСЕФХЈЖШВЛЕЭгк4(КСПЫ/СЂЗНУз)ЪБЃЌЫќВХФмЦ№ЕНОЛЛЏПеЦјЕФзїгУЃЎ
(1)ШєвЛДЮХчШї4ИіЕЅЮЛЕФОЛЛЏМСЃЌдђОЛЛЏЪБМфПЩДяМИЬьЃП
(2)ШєЕквЛДЮХчШї2ИіЕЅЮЛЕФОЛЛЏМСЃЌ6ЬьКѓдйХчШїa(1ЁмaЁм4)ИіЕЅЮЛЕФвЉМСЃЌвЊЪЙНгЯТРДЕФ4ЬьжаФмЙЛГжајгааЇОЛЛЏЃЌЪдЧѓaЕФзюаЁжЕ(ОЋШЗЕН0.1ЃЌВЮПМЪ§Он: ![]() ШЁ1.4)ЃЎ
ШЁ1.4)ЃЎ
ЁОД№АИЁП(1) 8;(2)1.6.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЬтжаЬѕМўУПХчШї1ИіЕЅЮЛЕФОЛЛЏМСЃЌПеЦјжаЪЭЗХЕФХЈЖШyЃЈЕЅЮЛЃККСПЫ/СЂЗНУзЃЉЫцзХЪБМф![]() (ЕЅЮЛЃКЬь)БфЛЏЕФКЏЪ§ЙиЯЕвбОИјГіЃЌдђвзЕУвЛДЮХчШї4ИіЕЅЮЛЕФОЛЛЏМСЪБЕФКЏЪ§ЙиЯЕЪНЃК
(ЕЅЮЛЃКЬь)БфЛЏЕФКЏЪ§ЙиЯЕвбОИјГіЃЌдђвзЕУвЛДЮХчШї4ИіЕЅЮЛЕФОЛЛЏМСЪБЕФКЏЪ§ЙиЯЕЪНЃК ![]() ЃЌетбљОЭЕУЕНвЛИіЗжЖЮКЏЪ§ЃЌЖдЗжЖЮКЏЪ§ЕФДІРэГЃгУЕФддђЃКЯШЗжПЊЃЌЯжКЯВЂЃЌНтСНИіВЛЕШЪНМДПЩЧѓНт; ЃЈ2ЃЉжаШєЕквЛДЮХчШї2ИіЕЅЮЛЕФОЛЛЏМСЃЌ6ЬьКѓдйХчШїaЃЈ
ЃЌетбљОЭЕУЕНвЛИіЗжЖЮКЏЪ§ЃЌЖдЗжЖЮКЏЪ§ЕФДІРэГЃгУЕФддђЃКЯШЗжПЊЃЌЯжКЯВЂЃЌНтСНИіВЛЕШЪНМДПЩЧѓНт; ЃЈ2ЃЉжаШєЕквЛДЮХчШї2ИіЕЅЮЛЕФОЛЛЏМСЃЌ6ЬьКѓдйХчШїaЃЈ![]() ЃЉИіЕЅЮЛЕФвЉМСЃЌИљОнЬтвтДгЕк6ЬьПЊЪМХЈЖШРДдДгыСНЗНУцЃЌетЪЧЬтжаЕФФбЕуЃЌЧАУцСєЯТЕФЮЊЃК
ЃЉИіЕЅЮЛЕФвЉМСЃЌИљОнЬтвтДгЕк6ЬьПЊЪМХЈЖШРДдДгыСНЗНУцЃЌетЪЧЬтжаЕФФбЕуЃЌЧАУцСєЯТЕФЮЊЃК ![]() ЃЌКѓУцаТдіЕФЮЊЃК
ЃЌКѓУцаТдіЕФЮЊЃК 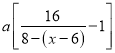 ЃЌЫљЕУЛЏМђМДПЩЕУЕНЃК
ЃЌЫљЕУЛЏМђМДПЩЕУЕНЃК ![]() ЃЌНсКЯЛљБОВЛЕШЪНжЊЪЖЧѓГізюаЁжЕ
ЃЌНсКЯЛљБОВЛЕШЪНжЊЪЖЧѓГізюаЁжЕ![]() ЃЌзюКѓНтвЛИіВЛЕШЪНЃК
ЃЌзюКѓНтвЛИіВЛЕШЪНЃК ![]() ЃЌМДПЩЧѓНтЃЎ
ЃЌМДПЩЧѓНтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉвђЮЊвЛДЮХчШї4ИіЕЅЮЛЕФОЛЛЏМСЃЌ
ЫљвдХЈЖШ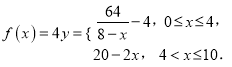
дђЕБ![]() ЪБЃЌгЩ
ЪБЃЌгЩ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЫљвдДЫЪБ
ЃЌЫљвдДЫЪБ![]() ЃЎ 3Зж
ЃЎ 3Зж
ЕБ![]() ЪБЃЌгЩ
ЪБЃЌгЩ![]() НтЕУ
НтЕУ![]() ЃЌЫљвдДЫЪБ
ЃЌЫљвдДЫЪБ![]() ЃЎ
ЃЎ
злКЯЕУ![]() ЃЌШєвЛДЮЭЖЗХ4ИіЕЅЮЛЕФжЦМСЃЌдђгааЇОЛЛЏЪБМфПЩДя8ЬьЃЎ 7Зж
ЃЌШєвЛДЮЭЖЗХ4ИіЕЅЮЛЕФжЦМСЃЌдђгааЇОЛЛЏЪБМфПЩДя8ЬьЃЎ 7Зж
ЃЈ2ЃЉЩшДгЕквЛДЮХчШїЦ№ЃЌОxЃЈ![]() ЃЉЬьЃЌ
ЃЉЬьЃЌ
ХЈЖШ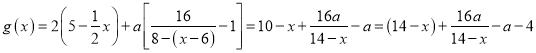 ЃЎ 10Зж
ЃЎ 10Зж
вђЮЊ![]() ЃЌЖј
ЃЌЖј![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌЙЪЕБЧвНіЕБ
ЃЌЙЪЕБЧвНіЕБ![]() ЪБЃЌyгазюаЁжЕЮЊ
ЪБЃЌyгазюаЁжЕЮЊ![]() .
.
Сю![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЫљвдaЕФзюаЁжЕЮЊ
ЃЌЫљвдaЕФзюаЁжЕЮЊ![]() ЃЎ 14Зж
ЃЎ 14Зж


 УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуMЃЈЉ1ЃЌ0ЃЉЃЌNЃЈ1ЃЌ0ЃЉЃЌЧњЯпEЩЯШЮвтвЛЕуЕНЕуMЕФОрРыОљЪЧЕНЕуNЕФОрРыЕФ![]() БЖЃЎ
БЖЃЎ
ЃЈ1ЃЉЧѓЧњЯпEЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊmЁй0ЃЌЩшжБЯп![]() ЃКxЉmyЉ1=0НЛЧњЯпEгкAЃЌCСНЕуЃЌжБЯп
ЃКxЉmyЉ1=0НЛЧњЯпEгкAЃЌCСНЕуЃЌжБЯп![]() ЃКmx+yЉm=0НЛЧњЯпEгкBЃЌDСНЕуЃЌШєCDЕФаБТЪЮЊЉ1ЪБЃЌЧѓжБЯпCDЕФЗНГЬЃЎ
ЃКmx+yЉm=0НЛЧњЯпEгкBЃЌDСНЕуЃЌШєCDЕФаБТЪЮЊЉ1ЪБЃЌЧѓжБЯпCDЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБШ§Ртжљ![]() жаЃЌ
жаЃЌ ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ ![]() ЃЌ
ЃЌ ![]() .
.
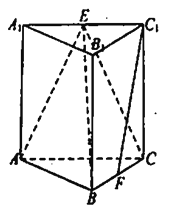
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєжБЯп![]() КЭЦНУц
КЭЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕЕШгк
ЫљГЩНЧЕФе§ЯвжЕЕШгк![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФЦНУцНЧЕФе§ЯвжЕ.
ЕФЦНУцНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁО2018КгФЯАВбєЪаИпШ§вЛФЃЁПШчЯТЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() жЎМфЕФвѕгАВПЗжМДЮЊ
жЎМфЕФвѕгАВПЗжМДЮЊ![]() ЃЌЧјгђ
ЃЌЧјгђ![]() жаЖЏЕу
жаЖЏЕу![]() ЕН
ЕН![]() ЕФОрРыжЎЛ§ЮЊ1ЃЎ
ЕФОрРыжЎЛ§ЮЊ1ЃЎ
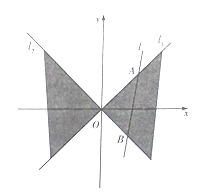
ЃЈЂёЃЉЧѓЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈЂђЃЉЖЏжБЯп![]() ДЉЙ§Чјгђ
ДЉЙ§Чјгђ![]() ЃЌЗжБ№НЛжБЯп
ЃЌЗжБ№НЛжБЯп![]() гк
гк![]() СНЕуЃЌШєжБЯп
СНЕуЃЌШєжБЯп![]() гыЙьМЃ
гыЙьМЃ![]() гаЧвжЛгавЛИіЙЋЙВЕуЃЌЧѓжЄЃК
гаЧвжЛгавЛИіЙЋЙВЕуЃЌЧѓжЄЃК ![]() ЕФУцЛ§КуЮЊЖЈжЕЃЎ
ЕФУцЛ§КуЮЊЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЄЗНаЮ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЪЧ
ЪЧ![]() жаЕуЃЈЭМ1ЃЉЃЎНЋЁї
жаЕуЃЈЭМ1ЃЉЃЎНЋЁї![]() би
би![]() елЦ№ЃЌЪЙЕУ
елЦ№ЃЌЪЙЕУ![]() ЃЈЭМ2ЃЉдкЭМ2жаЃК
ЃЈЭМ2ЃЉдкЭМ2жаЃК
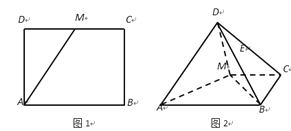
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]()
![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцЕу
ЩЯЪЧЗёДцЕу![]() ЃЌЪЙЕУЖўУцНЧ
ЃЌЪЙЕУЖўУцНЧ![]() ЮЊДѓаЁЮЊ
ЮЊДѓаЁЮЊ![]() ЃЌЫЕУїРэгЩЃЎ
ЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЯюЕШБШЪ§Са{an}(nЁЪN*)ЃЌЪзЯюa1ЃН3ЃЌЧАnЯюКЭЮЊSnЃЌЧвS3ЃЋa3ЁЂS5ЃЋa5ЃЌS4ЃЋa4ГЩЕШВюЪ§СаЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЪ§Са{nan}ЕФЧАnЯюКЭЮЊTnЃЌШєЖдШЮвте§ећЪ§nЃЌЖМгаTnЁЪ[aЃЌb]ЃЌЧѓbЃaЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕxOyжаЃЌжБЯпlЃКyЃНt(tЁй0)НЛyжсгкЕуMЃЌНЛХзЮяЯпCЃКy2ЃН2px(pЃО0)гкЕуPЃЌMЙигкЕуPЕФЖдГЦЕуЮЊNЃЌСЌНсONВЂбгГЄНЛCгкЕуH.
(1)Чѓ![]() ЃЛ
ЃЛ
(2)Г§HвдЭтЃЌжБЯпMHгыCЪЧЗёгаЦфЫќЙЋЙВЕуЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(2017ЁЄГЩЖМвЛея)вбжЊЭждВ![]() ЕФгвНЙЕуЮЊFЃЌЩшжБЯпlЃКxЃН5гыxжсЕФНЛЕуЮЊEЃЌЙ§ЕуFЧваБТЪЮЊkЕФжБЯпl1гыЭждВНЛгкAЃЌBСНЕуЃЌMЮЊЯпЖЮEFЕФжаЕуЃЎ
ЕФгвНЙЕуЮЊFЃЌЩшжБЯпlЃКxЃН5гыxжсЕФНЛЕуЮЊEЃЌЙ§ЕуFЧваБТЪЮЊkЕФжБЯпl1гыЭждВНЛгкAЃЌBСНЕуЃЌMЮЊЯпЖЮEFЕФжаЕуЃЎ
(1)ШєжБЯпl1ЕФЧуаБНЧЮЊ![]() ЃЌЧѓЁїABMЕФУцЛ§SЕФжЕЃЛ
ЃЌЧѓЁїABMЕФУцЛ§SЕФжЕЃЛ
(2)Й§ЕуBзїжБЯпBNЁЭlгкЕуNЃЌжЄУїЃКAЃЌMЃЌNШ§ЕуЙВЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаИпжаШЋЬхбЇЩњВЮМгФГЯюВтЦРЃЌАДЕУЗжЦРЮЊ![]() СНРрЃЈЦРЖЈБъзММћБэ1ЃЉЃЎИљОнФаХЎбЇЩњБШР§ЃЌЪЙгУЗжВуГщбљЕФЗНЗЈЫцЛњГщШЁСЫ10000УћбЇЩњЕФЕУЗжЪ§ОнЃЌЦфжаЕШМЖЮЊ
СНРрЃЈЦРЖЈБъзММћБэ1ЃЉЃЎИљОнФаХЎбЇЩњБШР§ЃЌЪЙгУЗжВуГщбљЕФЗНЗЈЫцЛњГщШЁСЫ10000УћбЇЩњЕФЕУЗжЪ§ОнЃЌЦфжаЕШМЖЮЊ![]() ЕФбЇЩњжага40%ЪЧФаЩњЃЌЕШМЖЮЊ
ЕФбЇЩњжага40%ЪЧФаЩњЃЌЕШМЖЮЊ![]() ЕФбЇЩњжагавЛАыЪЧХЎЩњЃЎЕШМЖЮЊ
ЕФбЇЩњжагавЛАыЪЧХЎЩњЃЎЕШМЖЮЊ![]() КЭ
КЭ![]() ЕФбЇЩњЭГГЦЮЊ
ЕФбЇЩњЭГГЦЮЊ![]() РрбЇЩњЃЌЕШМЖЮЊ
РрбЇЩњЃЌЕШМЖЮЊ![]() КЭ
КЭ![]() ЕФбЇЩњЭГГЦЮЊ
ЕФбЇЩњЭГГЦЮЊ![]() РрбЇЩњЃЎећРэет10000УћбЇЩњЕФЕУЗжЪ§ОнЃЌЕУЕНШчЭМ2ЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЌ
РрбЇЩњЃЎећРэет10000УћбЇЩњЕФЕУЗжЪ§ОнЃЌЕУЕНШчЭМ2ЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЌ
РрБ№ | ЕУЗжЃЈ | |
|
|
|
|
| |
|
|
|
|
| |
Бэ1
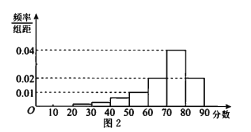
(I)вбжЊИУЪаИпжабЇЩњЙВ20ЭђШЫЃЌЪдЙРМЦдкИУЯюВтЦРжаБЛЦРЮЊ![]() РрбЇЩњЕФШЫЪ§ЃЛ
РрбЇЩњЕФШЫЪ§ЃЛ
(Ђђ)ФГ5ШЫЕУЗжЗжБ№ЮЊ45ЃЌ50ЃЌ55ЃЌ75ЃЌ85ЃЎДгет5ШЫжаЫцЛњбЁШЁ2ШЫзщГЩМззщЃЌСэЭт3ШЫзщГЩввзщЃЌЧѓЁАМзЁЂввСНзщИїга1Ућ![]() РрбЇЩњЁБЕФИХТЪЃЛ
РрбЇЩњЁБЕФИХТЪЃЛ
(Ђѓ)дкет10000УћбЇЩњжаЃЌФаЩњеМзмЪ§ЕФБШР§ЮЊ51%ЃЌ ![]() РрХЎЩњеМХЎЩњзмЪ§ЕФБШР§ЮЊ
РрХЎЩњеМХЎЩњзмЪ§ЕФБШР§ЮЊ![]() ЃЌ
ЃЌ ![]() РрФаЩњеМФаЩњзмЪ§ЕФБШР§ЮЊ
РрФаЩњеМФаЩњзмЪ§ЕФБШР§ЮЊ![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() гы
гы![]() ЕФДѓаЁЃЎЃЈжЛашаДГіНсТлЃЉ
ЕФДѓаЁЃЎЃЈжЛашаДГіНсТлЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com