
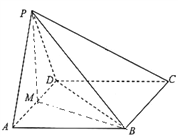
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为45°,求二面角
所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
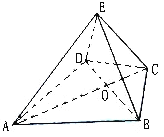
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)取BD中点O,连结CO,EO,推导出CO⊥BD,EO⊥BD,由此能证明BE=DE.
(2)以O为原点,OA为x轴,OB为y轴,OE为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣AE﹣D的余弦值.
试题解析:
证明:(1)取BD中点O,连结CO,EO,
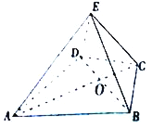
∵△BCD是等腰三角形,∠BCD=120°,∴CB=CD,∴CO⊥BD,
又∵EC⊥BD,EC∩CO=C,∴BD⊥平面EOC,∴EO⊥BD,
在△BDE中,∵O为BD的中点,∴BE=DE.
(2)∵平面EBD⊥平面ABCD,平面EBD∩平面ABCD=BD,
EO⊥BD,∴EO⊥平面ABCD,
又∵CO⊥BD,AO⊥BD,
∴A,O,C三点共线,AC⊥BD,
以O为原点,OA为x轴,OB为y轴,OE为z轴,建立空间直角坐标系,
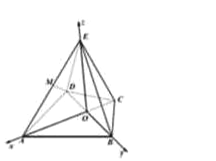
在正△ABD中,AB=2![]() ,∴AO=3,BO=DO=
,∴AO=3,BO=DO=![]() ,
,
∵直线AE与平面ABD所成角为45°,∴EO=AO=3,
A(3,0,0),B(0,![]() ,0),D(0,﹣
,0),D(0,﹣![]() ,0),E(0,0,3),
,0),E(0,0,3),
![]() =(﹣3,
=(﹣3,![]() ,0),
,0),![]() =(﹣3,﹣
=(﹣3,﹣![]() ,0),
,0),![]() =(﹣3,0,3),
=(﹣3,0,3),
设平面ABE的法向量![]() =(a,b,c),
=(a,b,c),
则![]() ,取a=1,得
,取a=1,得![]() =(1,
=(1,![]() ,1),
,1),
设平面ADE的法向量![]() =(x,y,z),
=(x,y,z),
则![]() ,取x=1,得
,取x=1,得![]() =(1,﹣
=(1,﹣![]() ,1),
,1),
设二面角B﹣AE﹣D为θ,
则cosθ=![]() =
=![]() =
=![]() .
.
∴二面角B﹣AE﹣D的余弦值为![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .过
.过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
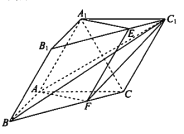
(l)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)记四棱锥![]() 的体积为
的体积为![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若曲线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且在点
,且在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,求实数
,求实数![]() 的值;
的值;
(2)记![]() 的导函数为
的导函数为![]() ,
, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() , 平面
, 平面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)证明: ![]() , 且
, 且![]() 与
与![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取100名学生,测得他们的身高(单位: ![]() ),按照区间
),按照区间![]() ,
,
![]() 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).

(1)求频率分布直方图中![]() 的值及身高在
的值及身高在![]() 以上的学生人数;
以上的学生人数;
(2)将身高在![]() 区间内的学生依次记为
区间内的学生依次记为![]() 三个组,用分层抽样的方法从这三个组中抽取6人,求从这三个组分别抽取的学生人数;
三个组,用分层抽样的方法从这三个组中抽取6人,求从这三个组分别抽取的学生人数;
(3)在(2)的条件下,要从6名学生中抽取2人.用列举法计算![]() 组中至少有1人被抽中的概率.
组中至少有1人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,令
,令![]() .
.
(Ⅰ)写出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在数列![]() ,使得
,使得![]() ?若存在,求出数列
?若存在,求出数列![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了活跃元旦晚会气氛,主持人请12位同学做一个游戏,第一轮游戏中,主持人将标有数字1到12的十二张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字7到12的卡片的同学留下,其余的淘汰;第二轮将标有数字1到6的六张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字4到6的卡片的同学留下,其余的淘汰;第三轮将标有数字1,2,3的三张相同的卡片放入一个不透明的盒子中,每人依次从中取出一张卡片,取到标有数字2,3的卡片的同学留下,其余的淘汰;第四轮用同样的办法淘汰一位同学,最后留下的这位同学获得一个奖品.已知同学甲参加了该游戏.
(1)求甲获得奖品的概率;
(2)设![]() 为甲参加游戏的轮数,求
为甲参加游戏的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com