
【题目】如图所示,在正方体![]() 中,
中, ![]() 是棱
是棱![]() 的中点.
的中点.
(![]() )求直线
)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(![]() )在棱
)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)先取AA1的中点M,连接EM,BM,根据中位线定理可知EM∥AD,而AD⊥平面ABB1A1,则EM⊥面ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,则∠EBM直线BE与平面ABB1A1所成的角,设正方体的棱长为2,则EM=AD=2,BE=3,于是在Rt△BEM中,求出此角的正弦值即可.
(2)在棱C1D1上存在点F,使B1F平面A1BE,分别取C1D1和CD的中点F,G,连接EG,BG,CD1,FG,因A1D1∥B1C1∥BC,且A1D1=BC,所以四边形A1BCD1为平行四边形,根据中位线定理可知EG∥A1B,从而说明A1,B,G,E共面,则BG面A1BE,根据FG∥C1C∥B1G,且FG=C1C=B1B,从而得到四边形B1BGF为平行四边形,则B1F∥BG,而B1F平面A1BE,BG平面A1BE,根据线面平行的判定定理可知B1F∥平面A1BE.
试题解析:
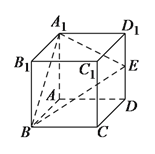
(![]() )如图(a),取
)如图(a),取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,因为
,因为![]() 是
是![]() 的中点,四边形
的中点,四边形![]() 为正方形,所以
为正方形,所以![]() ,
,
又在正方体![]() 中,
中, ![]() 平面
平面![]() ,所以
,所以![]() 面
面![]() ,从而
,从而![]() 为直线
为直线![]() 在平面
在平面![]() 上的射影,
上的射影,
![]() 直线
直线![]() 与平面
与平面![]() 所成的角.设正方体的棱长为
所成的角.设正方体的棱长为![]() ,则
,则![]() ,
, ![]() ,
,
于是在![]() 中,
中, ![]() ,
,
即:直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
(![]() )在棱
)在棱![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() ,
,
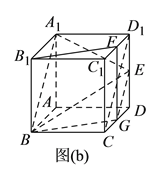
事实上,如图(b)所示,分别取![]() 和
和![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
因![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
因此![]() ,又
,又![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,所以
的中点,所以![]() ,从而
,从而![]() ,这说明
,这说明![]() ,
, ![]() ,
, ![]() ,
, ![]() 共面,
共面,
所以![]() 平面
平面![]() ,
,
因四边形![]() 与
与![]() ,皆为正方形
,皆为正方形![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
因此四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,而
,而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.



科目:高中数学 来源: 题型:
【题目】设锐角△ABC的三内角A、B、C所对边的边长分别为a、b、c,且 a=1,B=2A,则b的取值范围为( )
A.( ![]() ,
, ![]() )
)
B.(1, ![]() )
)
C.( ![]() ,2)
,2)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
, ![]() ,
, ![]() ,
, ![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(1)用![]() ,
,![]() 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内三个向量: ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1)
=(4,1)
(1)若( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),求实数k的值;
),求实数k的值;
(2)设 ![]() =(x,y),且满足(
=(x,y),且满足( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),|
),| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求
,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2013·湖北高考)四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且![]() =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且![]() =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且![]() =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com