
【题目】谢尔宾斯基三角形(Sierpinskitriangle)是一种分形几何图形,由波兰数学家谢尔宾斯基在1915年提出,它是一个自相似的例子,其构造方法是:
(1)取一个实心的等边三角形(图1);
(2)沿三边中点的连线,将它分成四个小三角形;
(3)挖去中间的那一个小三角形(图2);
(4)对其余三个小三角形重复(1)(2)(3)(4)(图3).
制作出来的图形如图4,图5,….

若图3(阴影部分)的面积为1,则图5(阴影部分)的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张,为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少0.5万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数量构成数列![]() ,每年发放电动型汽车牌照数为构成数列
,每年发放电动型汽车牌照数为构成数列![]() ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() 是等边三角形,
是等边三角形,![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点 .
的中点 .
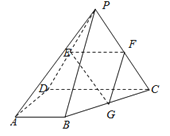
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
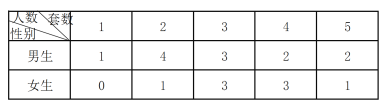
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试判断男学生完成套卷数的方差![]() 与女学生完成套卷数的方差
与女学生完成套卷数的方差![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在位于城市A南偏西![]() 相距100海里的B处,一股台风沿着正东方向袭来,风速为120海里/小时,台风影响的半径为
相距100海里的B处,一股台风沿着正东方向袭来,风速为120海里/小时,台风影响的半径为![]() 海里
海里
(1)若![]() ,求台风影响城市A持续的时间(精确到1分钟)?
,求台风影响城市A持续的时间(精确到1分钟)?
(2)若台风影响城市A持续的时间不超过1小时,求![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com