练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量y（千辆/小时）与汽车的平均速度v（千米/小时）之间的函数关系为：（）.

    （1）在该时段内，当汽车的平均速度为多少时，车流量最大？最大车流量为多少？（保留分数形式）

    （2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范用内？

    【答案】（1）当时，车流量最大，最大车流量约为千辆/时；（2）汽车的平均速度应大于且小于.

    【解析】

    （1）化简得，再利用基本不等式求解；

    （2）解不等式即得解.

    （1）依题得.

    当且仅当，即时，上时等号成立，

    （千辆/时）.

    当时，车流量最大，最大车流量约为千辆/时；

    （2）由条件得，因为，

    所以整理得，即，解得.

    如果要求在该时段内车流量超过10千辆/时，则汽车的平均速度应大于且小于.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】图是A，B两所学校艺术节期间收到的各类艺术作品的情况的统计图：

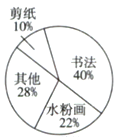
    A学校 B学校

    （1）从图中能否看出哪所学校收到的水粉画作品数量多？为什么？

    （2）已知A学校收到的剪纸作品比B学校的多20件，收到的书法作品比B学校的少100件，请问这两所学校收到艺术作品的总数分别是多少件？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    ①若有两个零点，则实数的取值范围是 ___________;

    ②若，则满足 的的取值范围是 _________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面四边形中，和都是等腰直角三角形且，正方形的边.

    （1）求证：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）设函数.

    (Ⅰ)讨论函数的单调性；

    (Ⅱ)当函数有最大值且最大值大于时，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

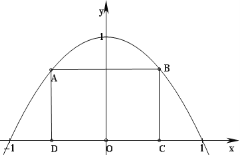
    【题目】如图所示，抛物线与轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在轴上.已知工业用地每单位面积价值为元，其它的三个边角地块每单位面积价值元.

    （1）求等待开垦土地的面积；

    （2）如何确定点C的位置，才能使得整块土地总价值最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极坐标系中，已知曲线：和曲线：，以极点为坐标原点，极轴为轴非负半轴建立平面直角坐标系.

    （1）求曲线和曲线的直角坐标方程；

    （2）若点是曲线上一动点，过点作线段的垂线交曲线于点，求线段长度的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把5件不同产品摆成一排．

    （1）若产品A必须摆在正中间，排法有多少种？

    （2）若产品A必须摆在两端，产品B不能摆在两端的排法有多少种？

    （3）若产品A与产品B相邻，且产品A与产品C不相邻，则不同的排法有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，是等边三角形，底面是直角梯形，，，是线段的中点，底面，已知.

    （1）求二面角的正弦值；

    （2）试在平面上找一点，使得平面.

    查看答案和解析>>

    同步练习册答案