
【题目】设m,n∈R,若直线(m+1)x+(n+1)y﹣2=0与圆(x﹣1)2+(y﹣1)2=1相切,则m+n的取值范围是( )
A.[1﹣ ![]() ,1+
,1+ ![]() ]
]
B.(﹣∞,1﹣ ![]() ]∪[1+
]∪[1+ ![]() ,+∞)
,+∞)
C.[2﹣2 ![]() ,2+2
,2+2 ![]() ]
]
D.(﹣∞,2﹣2 ![]() ]∪[2+2
]∪[2+2 ![]() ,+∞)
,+∞)
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的参数方程为![]() (θ为参数),直线l的极坐标方程为ρcos
(θ为参数),直线l的极坐标方程为ρcos![]() =2
=2![]() .
.
(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)求曲线C上的点到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
极坐标系与直角坐标系![]() 有相同的长度单位,以原点
有相同的长度单位,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴.曲线
轴正半轴为极轴.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,已知倾斜角为
,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)写出直线![]() 的参数方程;曲线
的参数方程;曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ![]() ,sinB=
,sinB= ![]() C.
C.
(1)求tanC的值;
(2)若a= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2![]() sin θ.
sin θ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A、B,若点P的坐标为(3,![]() ),求|PA|+|PB|.
),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() ,半径为4的圆C与直线l相切,圆心C在x轴上且在直线l的右上方.
,半径为4的圆C与直线l相切,圆心C在x轴上且在直线l的右上方.
(Ⅰ)求圆C的方程;
(Ⅱ)过点M (2,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查我市在校中学生参加体育运动的情况,从中随机抽取了16名男同学和14 名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下![]() 列联表:
列联表:
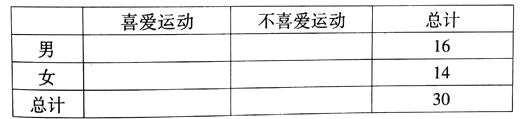
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
参考数据:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com