
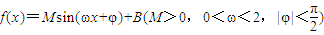 的一系列对应值如下表:
的一系列对应值如下表:| x |  | 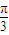 |  |  | 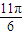 |  | 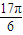 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
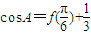 ,b=3c,求sinC.
,b=3c,求sinC. ,再利用余弦定理,求出
,再利用余弦定理,求出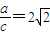 ,利用正弦定理可得结论.
,利用正弦定理可得结论. ,∴
,∴
 =2π,∴ω=
=2π,∴ω= =1
=1 代入可得sin(-
代入可得sin(-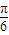 -φ)=-1
-φ)=-1 ,∴φ=
,∴φ=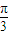
 …(4分)
…(4分)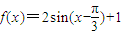 ,∴
,∴
 ,∴
,∴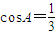 …(6分)
…(6分)
 ,∴
,∴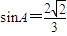
 ,∴
,∴ …(12分)
…(12分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 周期为
周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源:2011年广东省广州市仲元中学高三数学专题训练:三角函数(解析版) 题型:解答题
 的一系列对应值如下表:
的一系列对应值如下表:| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:2015届安徽省高一上学期第三次月考数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数 周期为
周期为 ,当
,当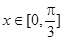 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下学期第一次月考数学试卷 题型:解答题
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数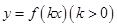 周期为
周期为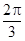 ,当
,当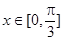 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数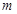 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com