
【题目】已知椭圆![]() :
: ![]() 的短轴长为2,且函数
的短轴长为2,且函数![]() 的图象与椭圆
的图象与椭圆![]() 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为线段
为线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 的一个公共点,求
的一个公共点,求![]() 面积的最小值,并求此时直线
面积的最小值,并求此时直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
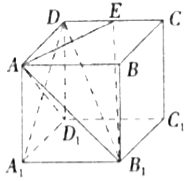
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个关于数列命题:
(1)若![]() 是等差数列,则三点
是等差数列,则三点![]() 、
、![]() 、
、![]() 共线;
共线;
(2)若![]() 是等比数列,则
是等比数列,则![]() 、
、![]() 、
、![]() (
(![]() )也是等比数列;
)也是等比数列;
(3)等比数列![]() 的前n项和为
的前n项和为![]() ,若对任意的
,若对任意的![]() ,点
,点![]() 均在函数
均在函数![]() (
(![]() ,
, ![]() 均为常数)的图象上,则r的值为
均为常数)的图象上,则r的值为![]() .
.
(4)对于数列![]() ,定义数列
,定义数列![]() 为数列
为数列![]() 的“差数列”,若
的“差数列”,若![]() ,
, ![]() 的“差数列”的通项为
的“差数列”的通项为![]() ,则数列
,则数列![]() 的前
的前![]() 项和
项和![]()
![]()
其中正确命题的个数是 ( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国好声音(![]()
![]()
![]()
![]() )》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
导师转身人数(人) | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)请列出所有的基本事件;
(2)求两人中恰好其中一位为其转身的导师不少于3人,而另一人为其转身的导师不多于2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)求该博物馆支付总费用的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com