
【题目】已知a∈R,函数f(x)满足f(2x)=x2﹣2ax+a2﹣1.
(Ⅰ)求f(x)的解析式,并写出f(x)的定义域;
(Ⅱ)若f(x)在 ![]() 上的值域为[﹣1,0],求实数a的取值范围.
上的值域为[﹣1,0],求实数a的取值范围.
【答案】解:(Ⅰ)令2x=t>0,则x=log2t,则 ![]() ,
,
即 ![]() .
.
定义域为:(0,+∞);
(Ⅱ)令g(x)=f(2x),则f(x)= ![]() ,
,
∴f(x)在 ![]() 上的值域为[﹣1,0]等价于g(x)=x2﹣2ax+a2﹣1
上的值域为[﹣1,0]等价于g(x)=x2﹣2ax+a2﹣1
在区间[a﹣1,a2﹣2a+2]上的值域为[﹣1,0].
∵g(a)=﹣1∈[﹣1,0],∴a∈[a﹣1,a2﹣2a+2],且g(x)在区间[a﹣1,a2﹣2a+2]上的最大值应在区间端点处取得.
又g(a﹣1)=0恰为g(x)在该区间上的最大值,故a必在区间右半部分,即 ![]() ,
,
解得 ![]() 或
或 ![]()
【解析】(Ⅰ)使用换元法令2x=t>0,则x=log2t代入即可求出;(Ⅱ)由题意,利用换元法将f(x)在 ![]() 上的值域为[﹣1,0]等价于g(x)=x2﹣2ax+a2﹣1在区间[a﹣1,a2﹣2a+2]上的值域为[﹣1,0].从而求解可得实数a的取值范围.
上的值域为[﹣1,0]等价于g(x)=x2﹣2ax+a2﹣1在区间[a﹣1,a2﹣2a+2]上的值域为[﹣1,0].从而求解可得实数a的取值范围.
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯(T.R.Malthus,1766—1834)就提出了自然状态下的人口增长模型: ![]() ,其中x表示经过的时间,
,其中x表示经过的时间, ![]() 表示x=0时的人口,r表示人口的平均增长率.
表示x=0时的人口,r表示人口的平均增长率.
下表是1950―1959年我国人口数据资料:

如果以各年人口增长率的平均值作为我国这一时期的人口增长率,用马尔萨斯人口增长模型建立我国这一时期的具体人口增长模型,某同学利用图形计算器进行了如下探究:
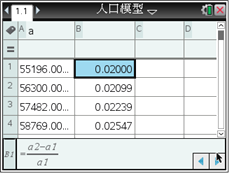
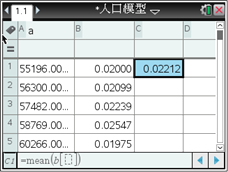
由此可得到我国1950―1959年我国这一时期的具体人口增长模型为____________. (精确到0.001)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=x﹣ln x﹣2.
(Ⅰ)求函数 f ( x)的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在区间(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=![]() ,其中2<m<2,m∈Z,满足:
,其中2<m<2,m∈Z,满足:
(1)f(x)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(x) +f(x)=0.
求同时满足条件(1)、(2)的幂函数f(x)的解析式,并求x∈[0,3]时,f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:(x﹣1)2+y2= ![]() ,椭圆C:
,椭圆C: ![]() +y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
+y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
A.2条
B.3条
C.4条
D.6条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象经过点![]() .
.
(1)求函数f(x)的解析式,并判断奇偶性;
(2)判断函数f(x)在(﹣![]() ,0)上的单调性,并用单调性定义证明.
,0)上的单调性,并用单调性定义证明.
(3)作出函数f(x)在定义域内的大致图象(不必写出作图过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆Γ: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= ![]() 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com