
【题目】已知数列![]() 满足对
满足对![]() 时,
时,![]() ,其对
,其对![]() ,有
,有![]() ,则数列
,则数列![]() 的前50项的和为__________.
的前50项的和为__________.
【答案】![]()
【解析】分析:由题意可得数列的前几项,可得数列{an}为周期为4的数列,且以1,2,3,2反复出现,运用等差数列的求和公式,计算可得所求和.
详解: 数列{an}满足对1≤n≤3时,an=n,且对n∈N*,有an+3+an+1=an+2+an,
可得a1=1,a2=2,a3=3,a4=1+3﹣2=2,
a5=2+2﹣3=1,a6=2,a7=3,a8=2,a9=1,a10=2,…,
则数列{an}为周期为4的数列,且以1,2,3,2反复出现,
可得数列{nan}的前50项的和为
(1+5+…+49)+2(2+6+…+50)+3(3+7+…+47)+2(4+8+…+48)
=![]() ×(1+49)×13+2×
×(1+49)×13+2×![]() ×(2+50)×13+3×
×(2+50)×13+3×![]() (3+47)×12+2×
(3+47)×12+2×![]() (4+48)×12
(4+48)×12
=2525.
故答案为:2525.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PA垂直于圆O所在的平面,M是圆周上任意一点,AN⊥PM,垂足为N , AE⊥PB,垂足为E .
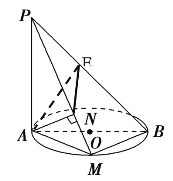
(1)求证:平面PAM⊥平面PBM.
(2)求证:![]() 是二面角A-PB-M的平面角.
是二面角A-PB-M的平面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润![]() 与投资金额x的函数关系为
与投资金额x的函数关系为![]() ,B产品的利润
,B产品的利润![]() 与投资金额x的函数关系为
与投资金额x的函数关系为![]() .(利润与投资金额单位:万元)
.(利润与投资金额单位:万元)
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出x的取值范围.
(2)怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设函数f(x)=(x-1)2+bln x,其中b为常数.
(1)当b>![]() 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(2)若函数f(x)有极值点,求b的取值范围及f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)点M在线段PC上,PM=tPC,试确定实数t的值,使得PA∥平面MQB.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用二分法求函数![]() 的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
A. 已经达到精确度的要求,可以取1.4作为近似值
B. 已经达到精确度的要求,可以取1.375作为近似值
C. 没有达到精确度的要求,应该接着计算f(1.4375)
D. 没有达到精确度的要求,应该接着计算f(1.3125)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com