
【题目】已知函数f(x)=sin(2x+![]() )+cos(2x﹣
)+cos(2x﹣![]() )+cos2x﹣sin2x,x∈R.
)+cos2x﹣sin2x,x∈R.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求函数f(x)在区间[﹣![]() ]上的最大值和最小值.
]上的最大值和最小值.
科目:高中数学 来源: 题型:
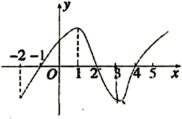
【题目】如图是![]() 的导函数
的导函数![]() 的图象,对于下列四个判断,其中正确的判断是( ).
的图象,对于下列四个判断,其中正确的判断是( ).
A.![]() 在
在![]() 上是增函数;
上是增函数;
B.当![]() 时,
时,![]() 取得极小值;
取得极小值;
C.![]() 在
在![]() 上是增函数、在
上是增函数、在![]() 上是减函数;
上是减函数;
D.当![]() 时,
时,![]() 取得极大值.
取得极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mx3+x﹣sinx(m∈R).
(1)当m=0时,(i)求y=f(x)在(![]() ,f(
,f(![]() ))处的切线方程;
))处的切线方程;
(ii)证明:f(x)<ex;
(2)当x≥0时,函数f(x)单调递减,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
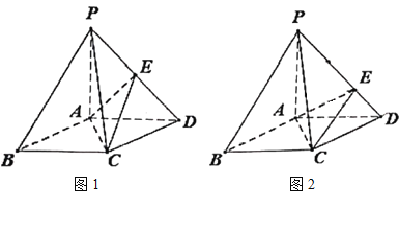
【题目】在底面是菱形的四棱锥![]() 中,
中,![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上.
上.
①如图1,若点![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
②如图2,若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l的极坐标方程为ρcosθ=4,曲线C的极坐标方程为ρ=2cosθ+2sinθ,以极点为坐标原点O,极轴为x轴的正半轴建立直角坐标系,射线l':y=kx(x≥0,0<k<1)与曲线C交于O,M两点.
(Ⅰ)写出直线l的直角坐标方程以及曲线C的参数方程;
(Ⅱ)若射线l′与直线l交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为维护交通秩序,防范电动自行车被盗,天津市公安局决定,开展二轮电动自行车免费登记、上牌照工作.电动自行车牌照分免费和收费(安装防盗装置)两大类,群众可以 自愿选择安装.已知甲、乙、丙三个不同类型小区的人数分别为15000,15000,20000.交管部门为了解社区居民意愿,现采用分层抽样的方法从中抽取10人进行电话访谈.
(Ⅰ)应从甲小区和丙小区的居民中分别抽取多少人?
(Ⅱ)设从甲小区抽取的居民为![]() ,丙小区抽取的居民为
,丙小区抽取的居民为![]() .现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
.现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
(ⅰ)试用所给字母列举出所有可能的抽取结果;
(ⅱ)设![]() 为事件“抽取的2人来自不同的小区”,求事件
为事件“抽取的2人来自不同的小区”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com