
【题目】如图,在三棱锥S﹣ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若AB=2 ![]() ,则此正三棱锥外接球的体积是( )
,则此正三棱锥外接球的体积是( )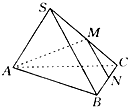
A.12π
B.4 ![]() π
π
C.![]() π
π
D.12 ![]() π
π
【答案】B
【解析】解:∵三棱锥S﹣ABC正棱锥,∴SB⊥AC(对棱互相垂直)∴MN⊥AC
又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球.
∴侧棱长为:2,
∴R= ![]() ,
,
∴正三棱锥外接球的体积是 ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】要得到函数y= ![]() sin2x+cos2x的图象,只需将函数y=2sin2x的图象( )
sin2x+cos2x的图象,只需将函数y=2sin2x的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数: ①f(x)=sin
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数: ①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: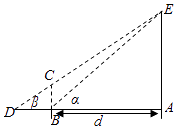
(1)若测得α=60°、β=30°,试求H的值;
(2)经过分析若干次测得的数据后,大家一致认为适当调整标杆到树木的距离d(单位:m),使α与β之差较大时,可以提高测量精确度.
若树木的实际高度为8m,试问d为多少时,α﹣β最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3.
,过焦点垂直长轴的弦长为3.
(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设(x1 , y1),(x2 , y2),…,(xn , yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( ) 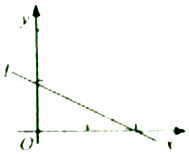
A.x和y的相关系数在﹣1和0之间
B.x和y的相关系数为直线l的斜率
C.当n为偶数时,分布在l两侧的样本点的个数一定相同
D.所有样本点(xi , yi)(i=1,2,…,n)都在直线l上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且在(0,+∞)上是增函数,设a=f(﹣ ![]() ),b=f(log3
),b=f(log3 ![]() ),c=f(
),c=f( ![]() ),则a、b、c的大小关系是( )
),则a、b、c的大小关系是( )
A.a<c<b
B.b<a<c
C.b<c<a
D.c<b<a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com